Analiza skupień (grupowanie obiektowe, ang. cluster analysis) jest zadaniem eksploracji danych, które polega na dzieleniu (zazwyczaj wielowymiarowego) zbioru danych na grupy w taki sposób, by elementy w tej samej grupie były do siebie podobne, a jednocześnie jak najbardziej odmienne od elementów z pozostałych grup. Analiza skupień znalazła wiele zastosowań w różnych dziedzinach, jak np. klasyfikacja dokumentów (WWW), odkrywanie grup klientów o podobnych zachowaniach (marketing), czy wykrywanie oszust kredytowych (banki).
Celem wykładu jest zapoznanie czytelników z najważnymi technikami grupowania danych, takimi jak grupowanie oparte na podziale i grupowanie hierarchiczne.
Zadanie analizy skupień obejmuje dwa związane ze sobą podzadania:
Drugie z tych podzadań mogłoby być w istocie potraktowane jako uczenie się opisów pojęć na podstawie przykładów, po uprzednim podzieleniu przykładów na grupy. W naszych rozważanich algorytmy realizują oba zadania łącznie.
Problem grupowania danych można sformułować jako problem optymalizacji kombinatorycznej. Niech dane będą:
Zadaniem jest podzielenie zbioru przykładów na grupy takie, żeby optymalizowały one funkcję jakości.
Możemy zindentyfikować trzy różne techniki analizy skupień:
Skoncentrujemy się na pierwszych dwóch technikach analizy skupień: grupowaniu opartym na podziale i grupowaniu hierarchicznym.
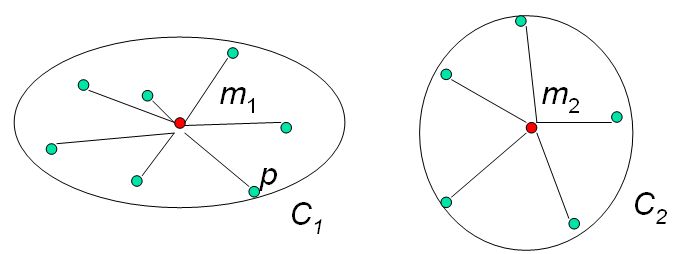
Zadaniem grupowania opartego na podziale jest podzielenie zbioru danych na k rozłącznych zbiorów elementów tak, aby elementy w każdym zbiorze były jak najbardziej jednorodne, tzn. dany jest zbiór przykładów P, naszym zadaniem jest znalezienie skupień C = {C1,...CK} takich, aby każdy element danych p ∈ P był jednoznacznie przypisany do jednego skupienia Ck.
Jednorodność jest zindentyfikowana przez stosowną funkcję oceny, taką jak odległości między każdym punktem a środkiem ciężkości skupienia, do którego został przypisany. Często środek ciężkości lub średnia punktów należących do skupienia jest uważana za reprezentatywny punkt tego skupienia.
Do mierzenia jakości grupowania można zastosować wiele różnych funkcji oceny. Jedną z najczęściej stosowanych funkcji jest funkcja zwana sumą błędów kwadratowych (ang. square error criterion):
|

gdzie mk jest środkiem ciężkości skupienia Ck, a d(.,.) jest funkcją odległości. W zależności od wyboru definicji odległości punktów, wyniki grupowania mogą się znacznie zmieniać. Najczęściej stosowanymi funkcjami odległości są:
|
|
|
|
Ogólna idea algorytmu K-means (MacQueen,1967) polega na tym, że rozpoczyna się od losowo wybranego grupowania punktów, następnie ponownie przypisuje się punkty tak, aby otrzymać największy wzrost (spadek) w funkcji oceny, po czym przelicza się zaktualizowane skupienia, po raz kolejny przypisuje się punkty i tak dalej aż do momentu, w którym nie ma już żadnych zmian w funkcji oceny lub w składzie skupień. To zachłanne podejście ma tę zaletę, że jest proste i gwarantuje otrzymanie co najmniej lokalnego maksimum (minimum) funkcji oceny. Metoda zapisana w postaci algorytmu jest pokazana na rysunku 1

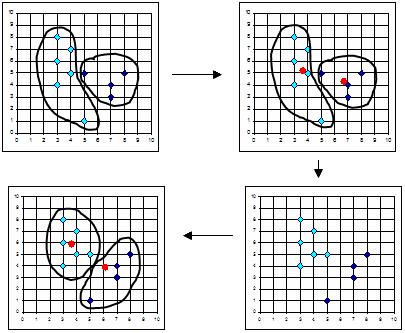
Kolejne kroki działania algorytmu można zobaczyć na rysunku 2
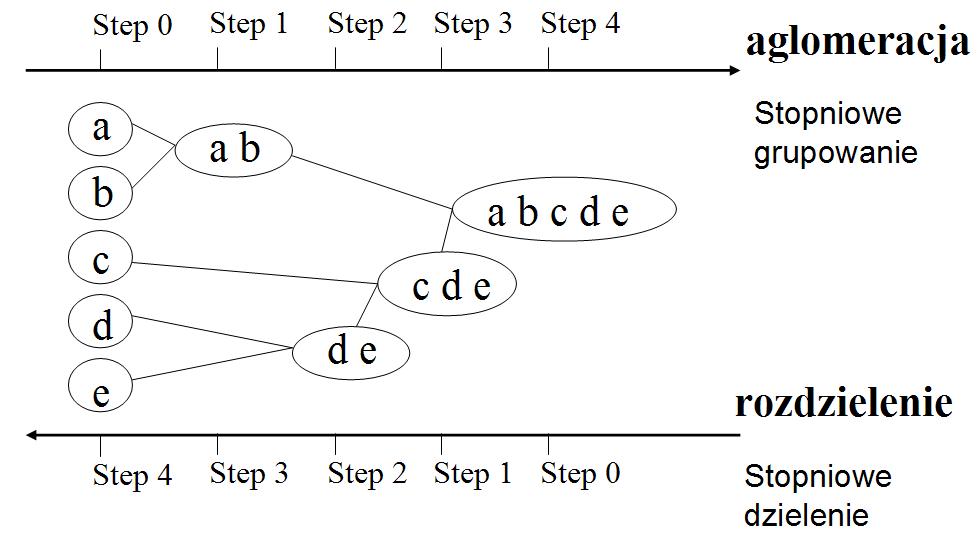
Podczas gdy metody analizy skupień oparte na podziale startują z określoną liczbą skupień i przeszukują różne rozmieszczenia punktów w skupieniach w celu znalezienia rozmieszczenia optymalizującego pewną funkcję oceny grupowania, metody hierarchiczne stopniowo łączą punkty lub dzielą nadskupienia. W rzeczywistości możemy na tej podstawie zidentyfikować dwa różne typy metod hierarchicznych: aglomeracyjne (które łączą punkty w coraz większe grupy) i rozdzielające (które dzielą grupy). Ilustrację tych metod znajdziemy na rysunku 3
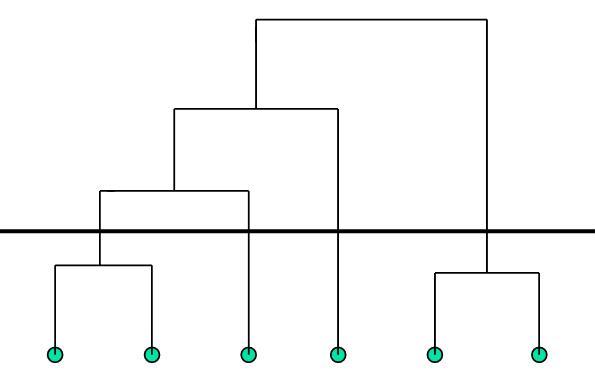
Hierarchiczne metody analizy skupień pozwalają na dogodne przedstawienie graficzne całej sekwencji łączenia (lub dzielenia) skupień. Z uwagi na podobieństwo do drzewa, takie przedstawienie jest zwanene dendrogramem. Grupy danych otrzymamy przez obcięcie dendrogramu na dowolnym poziomie (patrz rysunek 4).
Godną uwagi cechą grupowania hierarchicznego jest to, że nie ma pojęcia jawnej globalnej funkcji oceny. Zamiast tego są obliczane różne lokalne oceny par liści w drzewie (to znaczy par skupień danego hierarchicznego grupowania danych) w celu ustalenia, które pary skupień są najlepszymi kandydatami do aglomeracji (łączenia) lub rozdzielania (dzielenie). Zauważmy, że podobnie jak w przypadku globalnych funkcji oceny stosowanych przy grupowaniu opartym na podziale, różne lokalne funkcje oceny prowadzą do bardzo różnych grupowań danych.
Metody aglomeracyjne opierają się na miarach odległości między skupieniami. Zasadniczo przy zadanym grupowaniu wstępnym, w celu zredukowania liczby skupień łączą one te dwa skupienia, które są najbliżej siebie. Za każdym razem łączone są dwa najbliższe skupienia, a proces ten jest powtarzany do momentu, gdy istnieje tylko jedno skupienie zawierające wszystkie elementy danych. Zazwyczaj punktem początkowym dla tego procesu jest grupowanie, w którym każda grupa składa się z jednego elementu danych.
Aglomeracyjny algorytm grupowania danych jest pokazany na rysunku 2

Aglomeracyjny algorytm grupowania danych
Interpretacja algorytmu aglomeracyjnego jest pokazana na rysunku 5
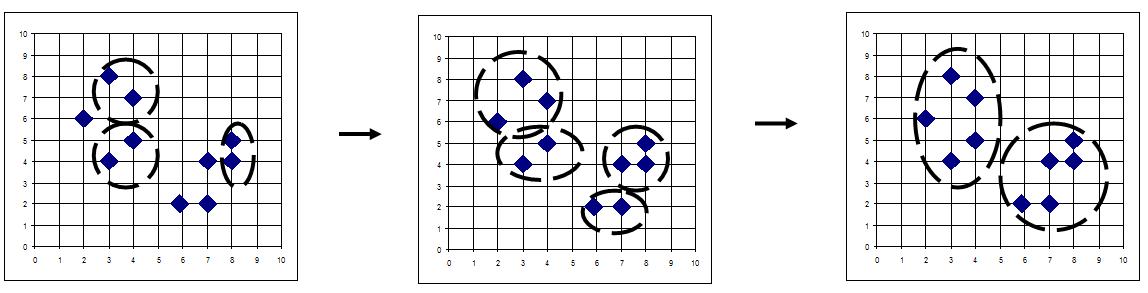
Metody rozdzielajace zaczynają od pojedynczego skupienia składającego się ze wszystkich punktów danych i szukają jego podziału na składniki. Te nowe składniki nastepnie dzielone i proces toczy się tak długo, aż każde skupienie będzie się składało z jednego elementu.
Rozdzielający algorytm grupowania danych jest pokazany na rysunku 3

Rozdzielający algorytm grupowania danych
Interpretacja algorytmu rozdzielającego jest pokazana na rysunku 6
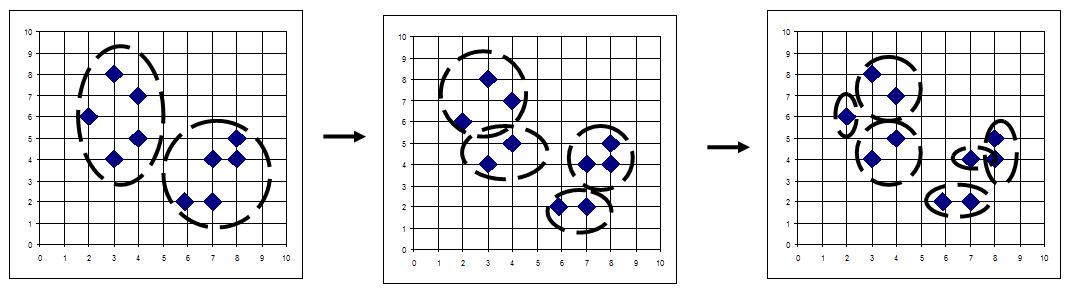
W ogólności metody rozdzielające są bardziej wymagające obliczeniowo i są na ogół stosowane w mniej szerokim zakresie niż metody aglomeracyjne.
Zauważmy, że przy grupowaniu aglomeracyjnym czy rozdzielajacym, potrzebne są odległości między grupami elementów danych. Niżej przedstawiono najważniejsze miary odległości między grupami elementów.
|
|
|
|