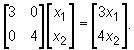
| « poprzedni punkt | następny punkt » |
Zauważmy, że w omówionym przykładzie obraz f([x1, x2]) dowolnego wektora [x1, x2] można zapisać w postaci macierzowej jako:
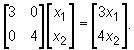
Przedstawimy teraz ogólną metodę znajdowania obrazu wektorów w przekształceniu liniowym. W pierwszym kroku określamy w jaki sposób transformują się wektory bazowe. Będzie to podstawą do określenia wartości przekształcenia liniowego dla dowolnego wektora z danej przestrzeni.
Niech baza B1 przestrzeni liniowej U składa się z wektorów:
e1, e2, ..., en
i baza B2 przestrzeni V składa się z wektorów:
h1, h2, ..., hm.
Określamy przekształcenia wektorów bazowych jako:
f (e1) = w1, f (e2) = w2 , ..., f (en) = wn.
Dowolny wektor v Î U wyrażamy za pomocą wektorów bazowych bazy B1:
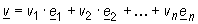 .
.
Współrzędne wektora wj w bazie B2 oznaczymy przez [ w1j, w2j, ..., wmj ]:
![]()
Wówczas:
![]()
![]()
![]()
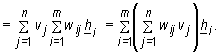
Tak więc współrzędne wektora f ( v ) w bazie B2 przestrzeni V maja postać:
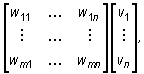
gdzie w macierzy powyżej współrzędne wektorów w1, w2,..., wn są ustawione w kolumnach.
Definicja
Macierz Af = [ wij ] składającą się ze współrzędnych wektorów f (e1), f (e2), ..., f (en) ustawionych w kolumnach nazywamy macierzą przekształcenia liniowego w bazach B1, B2. Jeżeli B1 = B2 to macierz Af nazywana jest macierzą przekształcenia w bazie B1.
Konstrukcja macierzy przekształcenia
Niech f oznacza przekształcenie liniowe.
Krok 1. Znajdujemy obrazy wektorów bazowych bazy B1:
f (e1) = w1, f (e2) = w2 , ..., f (en) = wn.
Krok 2. Tworzymy macierz Af przez wpisanie współrzędnych wektora wi w i - tej kolumnie macierzy.
Krok 3. Współrzędne wektora f ( v ) w bazie B2 są równe:
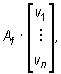
gdzie [ v1, v2, ..., vn ] są współrzędnymi wektora v w bazie B1.
Uwaga
Jeżeli U = Rn, V = Rm i w obu przestrzeniach rozpatrujemy bazy kanoniczne, to Af =[w1, w2,..., wn], gdzie wi = f ( ei ) jest zapisany jako i - ta kolumna oraz f ( v ) = Af × v, dla v Î Rn.
Jeżeli przy podaniu macierzy przekształcenia nie podane są bazy odpowiednich przestrzeni oznacza to, że rozpatrywane są odpowiednie bazy kanoniczne.
Przekształcenie liniowe jest jednoznacznie wyznaczone przez podanie macierzy przekształcenia liniowego dla ustalonych baz przestrzeni U i V. Okazuje się poza tym, że własności przekształceń liniowych można interpretować w terminach macierzy tego przekształcenia.
Przykład - macierz obrotu w R2.
Przekształcenie, w którym znajdujemy obraz punktu powstały w wyniku jego obrotu o kąt a, jest opisane wzorem:
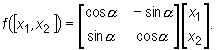
Zatem, macierz obrotu o kąt a ma postać:
![]()
Zauważmy, że det Af =1, zatem rząd Af = 2. Wynika to z tego, że obrazem przestrzeni R2 jest przy obrocie jest cała przestrzeń R2.
Uwaga
Jeżeli f jest przekształceniem liniowym określonym na wektorach w Rn o wartościach będących wektorami z Rm, to macierz Af jest wymiaru m x n.
| « poprzedni punkt | następny punkt » |