| następny punkt » |
Równania różniczkowe należą do kategorii równań funkcyjnych, czyli takich, w których niewiadomą jest funkcja. O ich specyfice decyduje to, że oprócz niewiadomej funkcji w równaniu występuje również pochodna (pochodne) tej funkcji.
Jeżeli w równaniu różniczkowym występuje tylko pochodna rzędu pierwszego, to równanie możemy symbolicznie zapisać w postaci
| F(x, y, y') = 0, |
gdzie F oznacza pewną funkcję trzech zmiennych, x jest zmienna niezależną, y poszukiwaną funkcją, zaś y' jej pochodną.
Przykłady
W dwóch pierwszych przypadkach pochodna występuje w równaniach w sposób uwikłany, trzecie równanie jest rozwikływalne ze względu na pochodną.
Rozważmy szczegółowo przypadek równania rozwikływalnego ze względu na pochodną, w którym niewiadoma funkcja y nie występuje explicite, Można je wówczas zapisać w postaci
| F(x, y') = 0, |
lub prościej
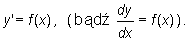 |
Rozwiązanie takiego równania jest równoważne wyznaczeniu całki nieoznaczonej funkcji f. Dowolna funkcja pierwotna funkcji f (o ile istnieje) jest rozwiązaniem równania. Zbiór rozwiązań tworzy całką nieoznaczoną funkcji f. Zatem każde rozwiązanie możemy zapisać w postaci
| y(x) = F (x) + C, |
gdzie F oznacza dowolną funkcję pierwotną funkcji f, C jest stałą rzeczywistą.
W teorii równań różniczkowych zbiór rozwiązań jest nazywany rozwiązaniem ogólnym, lub całką ogólną, zaś rozwiązywanie równania często jest nazywane całkowaniem równania.
Jeżeli zażądamy dodatkowo, by spełniony był warunek (zwany warunkiem początkowym)
| y(x0) = y0, |
to (jeśli jest on realizowalny) funkcja y będzie wyznaczona w sposób jednoznaczny przez dobór stałej C z równości
| y(x0) = F (x0) + C = y0, |
czyli
| C0 = y0 - F (x0). |
Wykorzystując pierwsze główne twierdzenie rachunku całkowego, funkcję y możemy zapisać w postaci
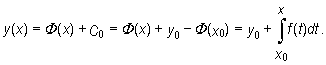 |
Jest to tzw. rozwiązanie szczególne równania, spełniające warunek początkowy y(x0) = y0.
Przykład
Rozwiązaniem równania
y' = ex
jest każda funkcja o postaci
y = ex + C.
Dla różnych wartości stałej C, funkcje te określają całkę ogólną równania. Ich wykresy tworzą rodzinę krzywych różniących się przesunięciem wzdłuż osi Oy.
Zadając warunek początkowy y(0) = 3 dostajemy
e0+ C = 3, czyli C = 2.
Stąd rozwiązanie szczególne równania spełniające warunek początkowy ma postać
y = ex + 2.
Wykresem tego rozwiązania jest krzywa przechodząca przez punkt o współrzędnych (0, 3).
Rys. 11.1
Uogólnieniem wprowadzonych pojęć są następujące definicje.
Definicja
Równaniem różniczkowym zwyczajnym nazywamy równanie
| F(x, y, y', y'', ..., y(n)) = 0, |
w którym niewiadomą jest funkcja y zmiennej x i w którym występują pochodne tej funkcji.
Przymiotnik "zwyczajne" oznacza, że funkcja niewiadoma zależy od jednej zmiennej. Równania różniczkowe, w których występują funkcje wielu zmiennych, noszą nazwę równań różniczkowych cząstkowych. W niniejszym wykładzie zajmować się będziemy wyłącznie równaniami zwyczajnymi.
Definicja
Liczbę n ³ 1 nazywamy rzędem równania różniczkowego, jeżeli w równaniu tym występuje pochodna rzędu n i nie występują pochodne rzędu wyższego niż n.
Przykłady
Definicja
Rozwiązaniem szczególnym (całką szczególną) równania różniczkowego na przedziale (a, b) nazywamy funkcję spełniającą to równanie w każdym punkcie tego przedziału.
Przykłady
ponieważ
(xex)' - xex = ex, dla każdego xÎ(-¥, ¥).
y' - y + x - 2 = 0.
Definicja
Zagadnieniem Cauchy'ego dla równania różniczkowego rzędu n nazywamy następujące zagadnienie:
Znaleźć rozwiązanie szczególne tego równania spełniające warunki początkowe
| y(x0) = y0, y'(x0) = y1, ... , y(n-1)(x0) = yn-1 |
gdzie liczby x0 oraz y0, y1, ... , yn-1, zwane wartościami początkowymi są dane.
W przypadku n = 1 warunek początkowy ma postać
| y(x0) = y0, |
dla n = 2
| y(x0) = y0, y'(x0) = y1. |
Przykład
Rozwiążemy zagadnienie Cauchy'ego dla równania różniczkowego rzędu 2
y'' = 6x,
z warunkami początkowymi y(0) = 0, y'(0) = 1.
Dwukrotnie całkując otrzymujemy
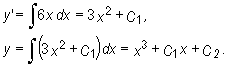
Z warunków początkowych dostajemy
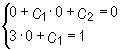
Stąd C1 = 1, C2 = 0 i rozwiązanie szczególne spełniające warunki początkowe ma postać y = x3 + x.
Definicja
Jeżeli każdemu układowi n liczb (C1, C2, ... , Cn) wybieranych dowolnie z pewnych przedziałów, jest przyporządkowana dokładnie jedna krzywa całkowa równania różniczkowego rzędu n, to mówimy, że jest określona rodzina krzywych całkowych tego równania zależna od n parametrów (C1, C2, ... ,Cn).
Definicja
Rozwiązaniem ogólnym (całką ogólną) równania różniczkowego rzędu n nazywamy rodzinę krzywych całkowych tego równania zależną od n parametrów (C1, C2, ... ,Cn), których wartości można tak dobrać, aby otrzymać krzywą całkową spełniającą warunki początkowe
| y(x0) = y0, y'(x0) = y1, ... , y(n-1)(x0) = yn-1, |
dla każdego układu wartości początkowych x0, y0, y1, ... , yn-1, dla których krzywa taka istnieje.
Przykład
Wykażemy, że dwuparametrowa rodzina funkcji
![]()
przedstawia całkę ogólną równania
![]()
Istotnie, obliczając drugą pochodną funkcji
![]()
i wstawiając ją do równania
![]()
łatwo sprawdzić, że każda funkcja z tej rodziny jest jego całką szczególną.
Ponadto, dla dowolnego układu wartości początkowych x0, y0, y1, możemy dobrać stałe C1, C2 tak, aby otrzymać całkę szczególną spełniającą warunki
![]() .
.
Mamy
![]()
![]()
Stąd
![]()
![]()
Szukaną całką szczególną spełniającą warunki
![]()
jest więc funkcja
![]()
Zatem wzór
![]()
przedstawia całkę ogólną rozważanego równania.
Zauważmy, że o ile definicja całki szczególnej jest oparta na pojęciu funkcji, to definicja całki ogólnej, eksponująca interpretację geometryczną rozwiązania równania różniczkowego, bazuje na pojęciu krzywej całkowej.
Oczywiście w przypadku gdy każda krzywa całkowa jest wykresem tylko jednej całki szczególnej (a więc funkcji), sformułowanie "rodzina krzywych całkowych" jest równoważne sformułowaniu "rodzina funkcji spełniających równanie różniczkowe". Krzywa całkowa może być wykresem jednej całki szczególnej (a więc funkcji - jak to miało miejsce w powyższym przykładzie), może też być łącznym wykresem większej ich liczby - nie będąc funkcją. Jak się przekonamy, rozwiązując zadania przykładowe, często otrzymujemy wyniki właśnie w postaci takich krzywych.
W dalszej części wykładu, zgodnie z powszechnie stosowaną terminologią, polecenie "rozwiązać równanie" będzie oznaczać wyznaczenie całki ogólnej tego równania.
Rozwiązanie zagadnienia Cauchy'ego uzyskamy wyznaczając całkę ogólną równania i dobierając występującą w nim stałą (stałe) tak, by spełniony był warunek początkowy (warunki początkowe).
Zanim przedstawimy metody rozwiązywania wybranych typów równań, odnotujmy kilka faktów dotyczących istnienia i jednoznaczności rozwiązań, nie objętych niniejszym wykładem.
| następny punkt » |