
|
| Rysunek 1: Christian Huygens (1629 - 1695) |
Jaka jest prawdziwa natura światła? Korpuskularna czy falowa? Istnieją zjawiska, np. fotoelektryczność i różne kolory światła, w których światło pokazuje swą naturę korpuskularną, czyli jakby światło było strumieniem cząstek. Ale inne zjawiska, takie jak interfrencja, dyfrakcja i załamanie światła bardzo trudno jest wytłumaczyć bez założenia o falowej naturze światła. Jak jest naprawdę? Fizyk odpowiada tak: to nie jest pytanie do mnie, mnie interesuje jaka teoria (model świata) najlepiej opisuje dane zjawisko.
| / | Fale | Kwanty |
| 1. | Interferencja | Fotoelektryczność |
| 2. | Dyfrakcja | Kolor |
| 3. | Refrakcja |
Tak więc, czy to pytanie dotyczy fizyki, a jeśli nie, to jakiej dziedziny nauki?

|
| Rysunek 1: Christian Huygens (1629 - 1695) |
Christian Huygens (1629 - 1695) - holenderski astronom i matematyk. Został zmuszony do opuszczenia Paryża na podstawie Edyktu Nantejskiego. Został zaproszony do Francji przez Colberta, a podczas swego pobytu we Francji odwiedzał Anglię i uzyskał tytuł Fellow of the Royal Society. Huygens dał podstawy falowej teorii światła i skonstruował zegar wahadłowy. Udoskonalił teleskop i odkrył prawdziwy kształt pierścieni Saturna. Prowadzone przez niego obserwacje astronomiczne zachęciły go do udoskonalenia pomiaru czasu.
Edykt Nantejski, wydany w 1598 r. przez króla Francji Henryka IV Burbona, wprowadzał wolność wyznania i równouprawnienie protestantów wobec katolików. Mogli odtąd budować swe kościoły oraz szkoły, zamki, urzędy, szpitale czy uniwersytety. Hugonoci (francuscy kalwiniści) mieli swobodę kultu z wyłączeniem Paryża. Edykt zakończył wojny religijne na terenie Francji oraz uregulował sytuację hugonotów. Edykt ten dawał hugonotom prawo do wolności politycznej oraz szereg twierdz (odebranych w roku 1528).
Ludwik XIV odwołał edykt w 1685 roku, co spowodowało załamanie protestantyzmu we Francji jako organizacji kościelnej i siły politycznej. Pełnię praw hugonotom przyznała dopiero rewolucja francuska w 1789 i Kodeks Napoleona.
http://www.maths.tcd.ie/pub/HistMath/People/Huygens/RouseBall/RB\_Huygens.html
Definicje - Jednostki wielkości optycznych
| Wielkość | Oznaczenie | Opis |
| Światłość | [cd] | kandela |
| Strumień świetlny | [lm] | |
| Ilość światła | [lm | lumenosekunda |
Podstawowe założenia optyki geometrycznej:
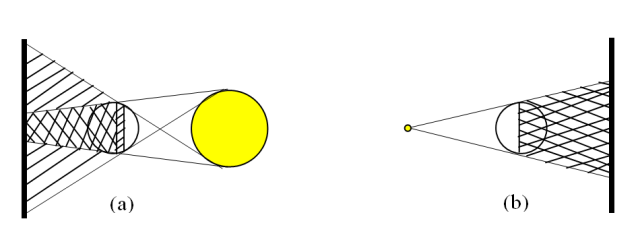
|
| Rysunek 2: Cienie rzucane przez źródła światła: (a) wielkość źródła światła większa od rozmiaru przeszkody, widać półcienie; (b) wielkość źródła światła mniejsza od rozmiaru przeszkody |
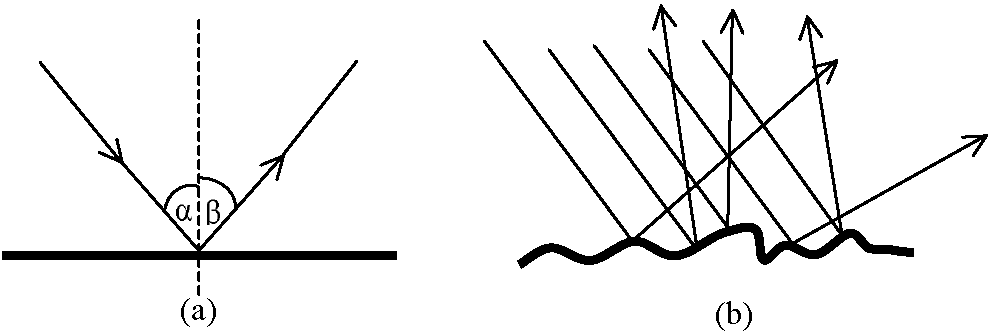
|
| Rysunek 3: Padanie światła na powierzchnię: (a) gładką; (b) pofałdowaną |
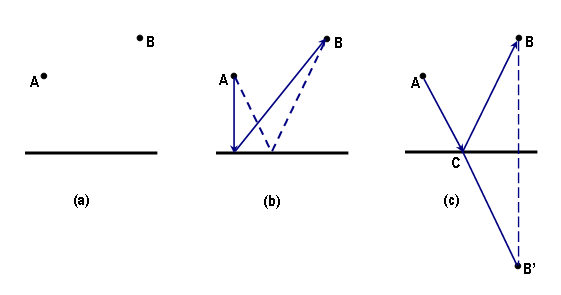
|
| Rysunek 4: Padanie światła na powierzchnię: (a) dwa punkty i nad powierzchnią odbijającą; (b) możliwe tory promieni światła pomiędzy punktami i po odbiciu; (c) zastosowanie zasady Fermata |
Pytanie 1: w jaki sposób światło może przebyć drogę od punktu do punktu ? (patrz rys. 4(a))
Odpowiedź 1: po linii prostej łączącej te punkty.
Pytanie 2: a co będzie, gdy światło po drodze musi się jeszcze odbić od zwierciadła? (patrz rys. 4(b))
Odpowiedź 2: odpowiedź jest nieco bardziej skomplikowana. Jeden z możliwych torów pokazany jest linią ciągłą. Po tym torze światło najszybciej dociera do zwierciadła, a potem biegnie po linii prostej do punktu . Jeśli przesuniemy punkt odbicia nieco w prawo (linia przerywana), to pierwszy odcinek ulegnie wydłużeniu, natomiast drugi skróci się. Całkowita droga też ulegnie skróceniu, a więc i czas potrzebny na przebycie tej drogi będzie krótszy.
Pytanie 3: gdzie leży prawdziwy punkt odbicia od zwierciadła? (patrz rys. 4(c))
Odpowiedź 3: po drugiej stronie zwierciadła zaznaczamy punkt , leżący w takiej samej odległości od zwierciadła jak punkt . Odcinek przecina zwierciadło w punkcie . To jest właśnie szukany prawdziwy punkt odbicia, gdyż droga z do przez jest najkrótsza, a wiec i najszybsza.
Analiza rys. 4(c) prowadzi do jeszcze jednego wniosku:
kąt padania jest równy kątowi odbicia
(patrz rys. 3a: kąt jest równy kątowi ).
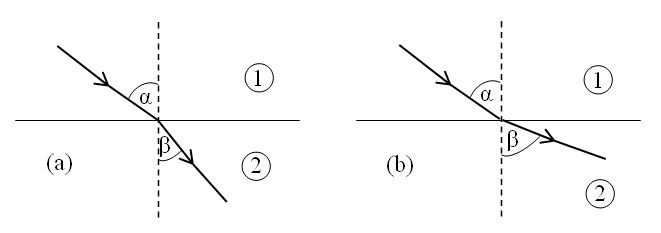
|
| Rysunek 5: Załamanie światła: (a) ku prostopadłej () ; (b) od prostopadłej () |
Promień świetlny przemieszczający się w ośrodku materialnym 1 z prędkością i padający na na granicę z innym ośrodkiem materialnym 2, w którym ma prędkość (np. z powietrza do wody), ulega częściowemu odbiciu, a reszta ulega załamaniu (następuje zmiana kierunku propagacji, patrz rys. 5). Kąt , zawarty pomiędzy kierunkiem promienia a normalną do powierzchni załamania, nazywamy kątem załamania, a promień w ośrodku 2 - promieniem załamanym.
Ważne: promień padający, normalna do powierzchni i promień załamany leżą w jednej płaszczyźnie.
Prawo załamania (Snellius, 1621)
| (1) |
| (2) |
gdzie - współczynnik załamania światła w ośrodku , - prędkość światła w próżni. W próżni współczynnik załamania , więc przy przejściu światła z próżni do ośrodka o współczynniku załamania , mamy
| (3) |
gdzie - bezwzględny współczynnik załamania.
|
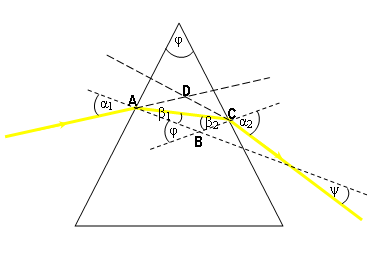
| Rysunek 6: Załamanie promienia światła w pryzmacie |
Pryzmat - ciało przezroczyste, w przekroju trójkąt równoramienny (wycięty z równoległościanu).
- kąt łamiący pryzmatu (kąt rozwarcia trójąta);
- kąt odchylenia;
- współczynnik załamania pryzmatu;
- współczynnik załamania otaczającego środowiska.
(na ogół )
Z prawa Sneliusa wynika, że
| (4) |
Z analizy trójkątów i wyciągamy wnioski, iż
| (5) |
| (6) |
Dla małych i (w radianach)
| (7) |
i wtedy
| (8) |
Dla powietrza , więc
| (9) |
Minimalne odchylenie promienia zachodzi dla i oczywiście , czyli (symetryczny bieg promieni)
| (10) |
Znamy: i , skąd wynika, że
| (11) |
| (12) |
Dla małych mamy ,
| (13) |
Newton (1666): światło białe (słoneczne) jest mieszaniną różnokolorowych promieni. Promień światła przechodząc przez pryzmat ulega rozszczepieniu.
|
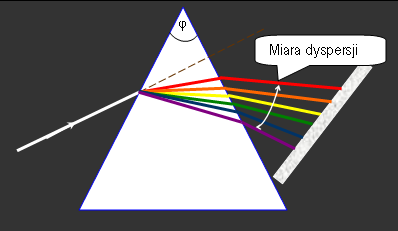
| Rysunek 7: Rozszczepienie światła |
Barwa światła zależy od długości fali, a więc każdej długości fali odpowiada inny współczynnik załamania.
Miara zdolności rozszczepiających materiałów: różnica współczynników załamania promieni czerwonych i fioletowych (średnia dyspersja pryzmatu).
Miara zdolności łamiących pryzmatu: wartość współczynnika załamania promienia żółtego.
Gdy promień świetlny przechodzi z ośrodka optycznie gęstszego (woda, szkło) o współczynniku załamania do ośrodka rzadszego optycznie (powietrze) o współczynniku załamania , to zgodnie z prawem Snelliusa
| (14) |
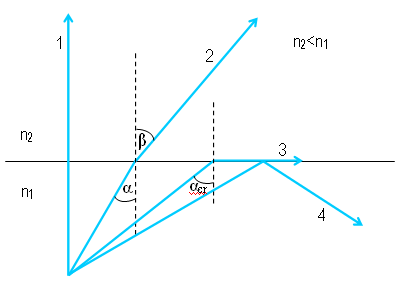
Ponieważ więc , czyli . Coraz większym kątom odpowiadają coraz większe kąty , ale zawsze . Kąt , dla którego kąt załamania nazywamy kątem granicznym. Dla kątów większych od kąta granicznego zachodzi całkowite wewnętrzne odbicie.
Przy przejściu światła z wody () do powietrza ()
| (15) |
czyli dla wody .
|
| Rysunek 8: Wewnętrzne odbicie |
|
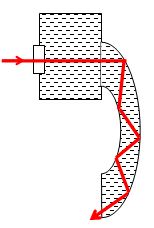
| Rysunek 9: Światłowód |
|
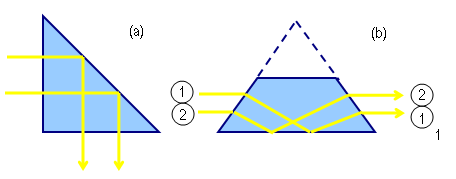
| Rysunek 10: Zjawisko całkowitego odbicia w pryzmacie: (a) zmiana kierunku biegu promieni o ; (b) zmiana kolejności biegu promieni (pryzmat Amici) |
|
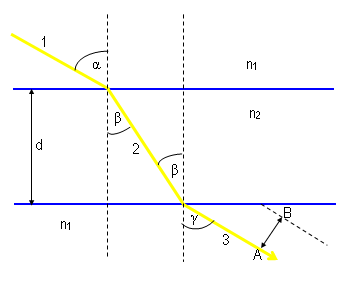
| Rysunek 11: Załamanie promienia światła w płytce płasko-równoległej |
Z prawa Snelliusa
| (16) |
Widać, że . Przesunięcie promienia AB zależy od grubości płytki , od kąta padania i od współczynników załamania i
| (17) |
Soczewki
|
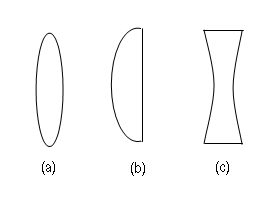
| Rysunek 12: Przykłady soczewek: (a) i (b) soczewki skupiające; (c) soczewka rozpraszająca |
Lupa
|
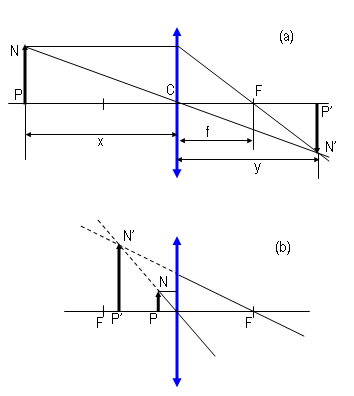
| Rysunek 13: Przykłady użycia soczewki skupiającej: (a) przedmiot w odległości większej od ogniskowej soczewki; (b) przedmiot w odległości mniejszej od ogniskowej soczewki |
|
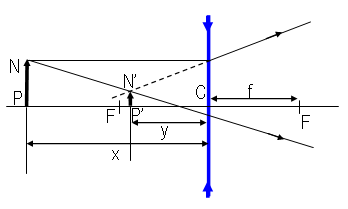
| Rysunek 14: Bieg promieni w soczewce rozpraszającej |
|
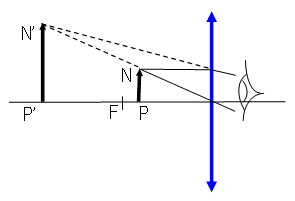
| Rysunek 15: Bieg promieni w lupie |
Lupa: soczewka skupiająca o małej ogniskowej (dużej zdolności skupiającej ). Przedmiot PN ustawia się miedzy ogniskiem a soczewką tak, aby obraz P'N' (urojony, powiększony, prosty) powstał w odległości dobrego widzenia oka , znajdującego się po drugiej stronie soczewki i blisko niej (Rys. 15).
Powiększenie wynosi
| (18) |
Ze wzoru soczewkowego
| (19) |
| (20) |
| (21) |
Obraz powstaje po tej samej stronie soczewki co przedmiot, więc , , ale . W związku z tym , czyli obraz jest urojony, nie odwrócony, ponieważ . Obraz jest tym bardziej powiększony im mniejsza jest ogniskowa. Np., lupa o ogniskowej cm daje sześciokrotne powiększenie
Aby uzyskać powiększenie 11-krotne, należy użyć lupy o ogniskowej cm.
1. Odpowiedz na pytania:
i. Jaka jest prawdziwa natura światła: falowa czy korpuskularna? Ile czasu trwa już dyskusja na ten temat?
ii. Kiedy pojawiają się półcienie?
iii. Czy w zjawisku załamania światła kąt załamania może być większy od kąta padania?
iv. Dlaczego w pryzmacie następuje rozszczepienie światła?
v. Jakie zjawisko wykorzystuje się w światłowodach?
vi. Jaki jest związek ofniskowej soczewki z uzyskiwanym za jej pomocą powiększeniem?
2. Sformułuj podstawowe prawa optyki geometrycznej.
3. Wyprowadź wzór na wspólczynnik załamania pryzmatu.
4. Wyprowadź wzór na przesunięcie promienia w płytce płasko-równoległej.