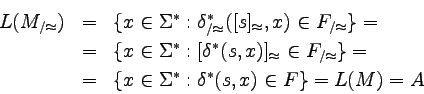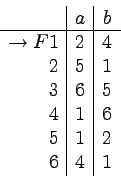W tym wykładzie zajmiemy się problemem minimalizacji liczby
stanów w deterministycznych automatach skończonych.
Konstruując automaty skończone często możemy dość do kilu
rozwiązań o różnej liczbie stanów.
Jak znaleźć automat o najmniejszej możliwej liczbie stanów?
W przypadku deterministycznych automatów skończonych
znany jest efektywny algorytm przekształcający dowolny
automat akceptujący dany język w automat o minimalnej liczbie
stanów.
Zanim poznamy ten algorytm i udowodnimy jego poprawność,
zobaczmy na przykładzie jak można zminimalizować liczbę stanów.
Przykład
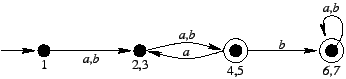
Weźmy na początek niedeterministyczny automat skończony
akceptujący te słowa (nad alfabetem
{a,b}), które
zawierają podsłowo
aab.
Automat ten ma 4 stany, a więc odpowiadający mu automat
potęgowy ma 16 stanów.
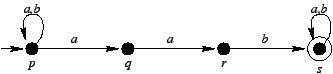
Oczywiście możemy się ograniczyć do stanów osiągalnych,
a tych jest 6.
Zauważmy, że możemy skleić ze sobą wszystkie stany akceptujące --
po ich osiągnięciu nie można już ich opuścić, a więc
słowo musi zostać zaakceptowane.
Uzyskaliśmy automat deterministyczny o 4 stanach.
Czy to jest minimum?
Zastanówmy się ile stanów jest niezbędnych.
Potrzebny jest jeden stan akceptujący, do którego wchodzimy,
gdy wczytamy podsłowo aab.
Dodatkowo potrzebujemy przynajmniej 3 inne stany.
Możemy je rozróżnić m.inn. po najkrótszych słowach
koniecznych do osiągnięcia stanu akceptującego.
Dla stanu początkowego jest to oczywiście słowo aab.
Dla stanu w jakim jesteśmy po wczytaniu a jest to ab,
a dla stanu, w którym jesteśmy po wczytaniu aa jest to b.
Razem uzyskujemy 4 stany, a więc nasz automat jest minimalny.
Jak widać z powyższego przykładu niektóre stany w automacie
deterministycznym mogą być sobie ,,równoważne'' i możemy je
skleić.
Natomiast badając, czy stany są równoważne powinniśmy zwrócić
uwagę na to jakie słowa z danych stanów prowadzą do stanów
akceptujących.
Jeśli są tu jakieś różnice, to stanów nie możemy sklejać.
Narazie są to mało precyzyjne intuicje, ale za chwilę
sformalizujemy je.
Nadal jednak pozostaje otwarte pytanie, czy usunięcie stanów
nieosiągalnych i sklejenie stanów ,,równoważnych'' prowadzi do
jednego automatu minimalnego?
Czy też zaczynając od różnych automatów możemy uzyskać różne
automaty minimalne?
Pokażemy, że dla każdego języka regularnego istnieje jeden
(z dokładnością do izomorfizmu) minimalny deterministyczny
automat skończony.
Definicja
Niech
A będzie ustalonym językiem.
Przez
A/x oznaczamy język postaci:
Języki postaci A/x dla
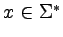 nazywamy
językami ilorazowymi.
nazywamy
językami ilorazowymi.
Inaczej mówiąc, A/x to język złożony ze wszystkich tych ciągów
dalszych, które uzupełniają wystąpienia prefiksów x w słowach
z A.
W szczególności
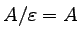 .
Wprost z definicji języka A/x wynika następujący fakt:
.
Wprost z definicji języka A/x wynika następujący fakt:
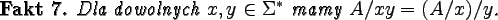
Stąd zaś wynika kolejny fakt:
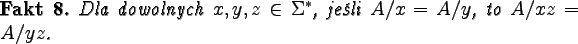
Jest tak gdyż:
A/xz = (A/x)/z = (A/y)/z = A/yz
Jeżeli dodatkowo A jest regularny to pojawiają się dodatkowe
intuicje.
Niech
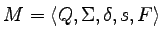 będzie deterministycznym
automatem skończonym akceptujący A, L(M) = A, w którym
wszystkie stany są osiągalne.
A/x to język złożony z tych słów, które prowadzą ze stanu
będzie deterministycznym
automatem skończonym akceptujący A, L(M) = A, w którym
wszystkie stany są osiągalne.
A/x to język złożony z tych słów, które prowadzą ze stanu
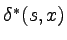 do stanów akceptujących,
(czyli jest to język akceptowany przez automat postaci
do stanów akceptujących,
(czyli jest to język akceptowany przez automat postaci
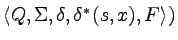 .
Ponieważ to, jakie słowa prowadzą z danego stanu do stanów
akceptujących zależy od tego stanu, ale nie od tego jak
dostaliśmy się do tego stanu, więc
zachodzi następujący fakt:
.
Ponieważ to, jakie słowa prowadzą z danego stanu do stanów
akceptujących zależy od tego stanu, ale nie od tego jak
dostaliśmy się do tego stanu, więc
zachodzi następujący fakt:
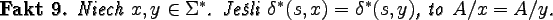
Możemy więc każdemu stanowi q automatu M przyporządkować
jeden z języków ilorazowych A/x języka A --
dokładnie taki, dla którego
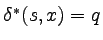 .
Wynika stąd kolejny fakt:
.
Wynika stąd kolejny fakt:
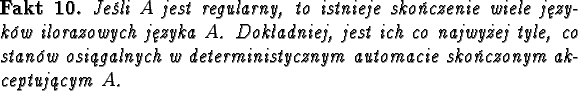
Okazuje się, że odwrotna implikacja jest również prawdziwa.
![\begin{theorem}[uproszczone twierdzenie Myhilla-Nerode'a]
Niech $A$ będzie ust...
... skończenie wiele języków ilorazowych
języka $A$.
\end{itemize} \end{theorem}](jfa-main-img481.png)
Implikacja w jedną stronę wynika z poprzedniego faktu.
Musimy pokazać, że jeżeli istnieje skończenie wiele języków ilorazowych
języka A, to A jest regularny.
Skonstruujemy deterministyczny automat skończony akceptujący
A.
Stanami tego automatu będą języki ilorazowe języka A,
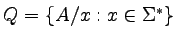 .
Nasz automat skonstruujemy tak, że każdy stan jako język
będzie zawierał dokładnie te słowa, które z tego stanu
prowadzą do stanów akceptujących:
.
Nasz automat skonstruujemy tak, że każdy stan jako język
będzie zawierał dokładnie te słowa, które z tego stanu
prowadzą do stanów akceptujących:
Stanem początkowym jest oczywiście
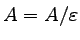 ,
gdyż nasz automat ma akceptować właśnie język A.
Stanami akceptującymi są te stany, które jako języki zawierają
słowo puste,
,
gdyż nasz automat ma akceptować właśnie język A.
Stanami akceptującymi są te stany, które jako języki zawierają
słowo puste,
Czyli:
Natomiast funkcja przejścia jest postaci:
Powyższa definicja jest poprawna, gdyż
jeśli A/x = A/y, to A/xa = A/ya.
Trzeba jeszcze pokazać, że automat
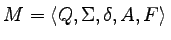 akceptuje język A.
Niech
akceptuje język A.
Niech
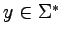 ,
,
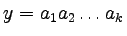 .
Zauważmy, że:
.
Zauważmy, że:
Stąd, język akceptowany przez M to:

Zauważmy, że automat skonstruowany w powyższym dowodzie ma
minimalną liczbę stanów -- gdyż ma ich dokładnie tyle ile jest
języków ilorazowych języka A.
Pokażemy jak z dowolnego deterministycznego automatu skończonego
akceptującego język A zrobić automat izomorficzny ze
skonstruowanym powyżej.
Niech
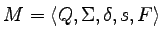 będzie dowolnym ustalonym
deterministycznym automatem skończonym akceptującym język A,
L(M) = A, w którym wszystkie stany są osiągalne.
(Jeśli M zawiera stany nieosiągalne, to najpierw je
usuwamy.)
Każdemu stanowi
będzie dowolnym ustalonym
deterministycznym automatem skończonym akceptującym język A,
L(M) = A, w którym wszystkie stany są osiągalne.
(Jeśli M zawiera stany nieosiągalne, to najpierw je
usuwamy.)
Każdemu stanowi 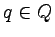 możemy przypisać język złożony z
tych słów, które prowadzą z q do stanów akceptujących.
Język taki to A/x, gdzie x prowadzi z s do q,
możemy przypisać język złożony z
tych słów, które prowadzą z q do stanów akceptujących.
Język taki to A/x, gdzie x prowadzi z s do q,
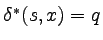 .
.
Niech 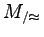 będzie
automatem powstałym z M przez sklejenie ze sobą stanów,
którym przypisaliśmy takie same języki ilorazowe.
Ściśle rzecz biorąc, na stanach automatu M definiujemy
relację równoważności
będzie
automatem powstałym z M przez sklejenie ze sobą stanów,
którym przypisaliśmy takie same języki ilorazowe.
Ściśle rzecz biorąc, na stanach automatu M definiujemy
relację równoważności
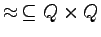 określoną w następujący sposób:
określoną w następujący sposób:
Inaczej mówiąc, niech A/x i A/y będą językami ilorazowymi
przypisanymi
stanom p i q, wówczas 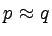 wtw., gdy A/x = A/y.
wtw., gdy A/x = A/y.
Sklejamy te stany automatu M, które są sobie równoważne:
gdzie:
Automat 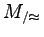 jest nazywany automatem ilorazowym.
jest nazywany automatem ilorazowym.
Po pierwsze musimy się upewnić, czy
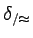 jest poprawnie
zdefiniowana.
Musimy w tym celu pokazać, że jeżeli sklejamy ze sobą dwa
stany
jest poprawnie
zdefiniowana.
Musimy w tym celu pokazać, że jeżeli sklejamy ze sobą dwa
stany 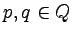 ,
, 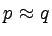 , to dla dowolnego
, to dla dowolnego 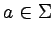 mamy również
mamy również
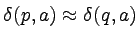 .
Skoro
.
Skoro 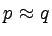 , to A/x = A/y, a zatem
A/xa = A/ya, czyli
, to A/x = A/y, a zatem
A/xa = A/ya, czyli
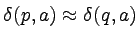 .
.
Zauważmy, że nigdy nie skleimy stanu akceptującego z nieakceptującym,
gdyż stany akceptujące charakteryzują się tym, że przypisane im
języki zawierają słowa puste.
Czy automat 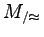 akceptuje ten sam język co M,
akceptuje ten sam język co M,
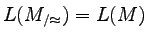 ?
Można pokazać (przez indukcję), że dla dowolnego stanu
?
Można pokazać (przez indukcję), że dla dowolnego stanu
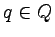 i słowa
i słowa
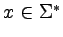 mamy
mamy
![$\delta_{/\approx}^*([q]_\approx, x) = [\delta^*(q, x)]_\approx$](jfa-main-img504.png) .
Ponieważ jednak nie skleiliśmy żadnego stanu akceptującego z
żadnym ze stanów nieakceptujących, mamy:
.
Ponieważ jednak nie skleiliśmy żadnego stanu akceptującego z
żadnym ze stanów nieakceptujących, mamy:
Tak więc usuwając stany nieosiągalne i sklejając ze sobą stany,
którym odpowiadają te same języki ilorazowe otrzymujemy
ten sam minimalny deterministyczny automat skończony akceptujący
dany język regularny.
Przykład
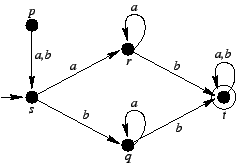
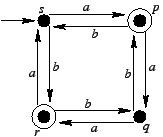
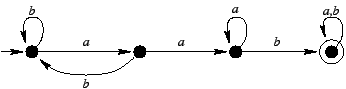
Weźmy następujący automat deterministyczny:
Stan p jest nieosiągalny.
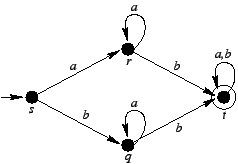
Po jego usunięciu mamy:
Tylko dwa stany możemy skleić ze sobą: r i q,
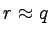 .
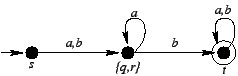
Po ich sklejeniu uzyskujemy;
.
Po ich sklejeniu uzyskujemy;
Pokażemy jak można zaimplementować opisaną w poprzednim
punkcie konstrukcję.
Algorytm minimalizacji składa się z dwóch faz:
- usunięcia stanów nieosiągalnych,
- wyznaczenia relacji równoważności
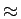 i
sklejenia ze sobą stanów równoważnych.
i
sklejenia ze sobą stanów równoważnych.
Znalezienie stanów nieosiągalnych jest prostsze.
Trudniej natomiast znaleźć stany równoważne.
Przypomnijmy, że dwa stany p i q są sobie równoważne, gdy:
Pokażemy algorytm, który znajduje wszystkie pary nierównoważnych
sobie stanów.
Siłą rzeczy, pozostałe pary stanów są sobie równoważne i można
je skleić ze sobą.
Jeśli stany p i q nie są sobie równoważne, to
istnieje rozróżniające je słowo x, takie że:
Początkowo zakładamy, że wszystkie stany można skleić ze sobą.
Następnie sukcesywnie wyznaczamy pary stanów które nie są sobie
równoważne -- w kolejności wg. rosnącej długości najkrótszych
rozróżniających je słów.
- Tworzymy tablicę wartości logicznych T{p,q}
indeksowaną nieuporządkowanymi parami {p,q} stanów
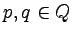 .
Początkowo
T{p,q} = true dla wszystkich
.
Początkowo
T{p,q} = true dla wszystkich
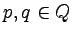 .
.
- Dla wszystkich takich par stanów {p,q}, że
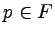 i
i 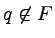 zaznaczamy
T{p,q} = false.
Jeśli p jest akceptujący, a q nie, to stany te
rozróżnia słowo puste
zaznaczamy
T{p,q} = false.
Jeśli p jest akceptujący, a q nie, to stany te
rozróżnia słowo puste 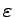 .
.
- Dla wszystkich par stanów {p,q} i znaków
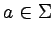 takich, że
takich, że
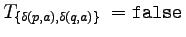 ,
zaznaczamy również
T{p,q} = false.
,
zaznaczamy również
T{p,q} = false.
- Jeżeli w kroku 3 zmieniliśmy choć jedną komórkę
tablicy T z true na false, to
powtarzamy krok 3 -- tak długo, aż nie będzie on
powodował żadnych zmian w tablicy T.
- Na koniec mamy:
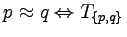 .
.
Poprawność algorytmu wynika stąd, że dla każdej pary stanów
{p,q}, które nie są sobie równoważne istnieje pewne słowo,
które je rozróżnia.
Weźmy najkrótsze takie słowo.
W kroku 2 wyznaczamy wszystkie takie pary, które są
rozróżniane przez 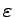 .
Z każdym powtórzeniem kroku 3 wyznaczamy wszystkie takie pary,
które są rozróżniane przez słowa o jeden dłuższe.
.
Z każdym powtórzeniem kroku 3 wyznaczamy wszystkie takie pary,
które są rozróżniane przez słowa o jeden dłuższe.
Ponieważ tablica T ma skończoną liczbę komórek, więc krok 3
jest powtarzany ograniczoną liczbę razy, a powyższy algorytm
zawsze się zatrzyma.
Przykład
Weźmy następujący automat deterministyczny:
Wszystkie stany są osiągalne.
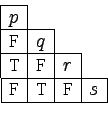
Tablica T obliczona dla tego automatu uzyskuje swą postać
już w kroku 2:
Co oznacza, że możemy skleić ze sobą stany s i q oraz p
i r:
Przykład
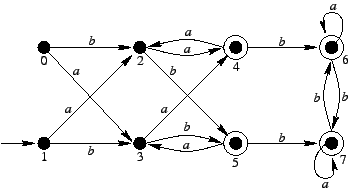
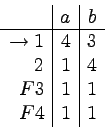
Weźmy następujący automat deterministyczny:
Stan 0 jest nieosiągalny.
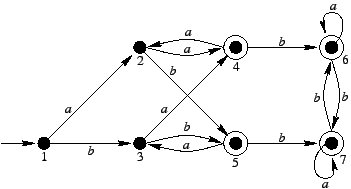
Po jego usunięciu mamy:
Tablica T obliczona dla tego automatu uzyskuje swą ostateczną postać po jednokrotnej iteracji kroku 3:
Co oznacza, że możemy skleić ze sobą stany:
2 z 3, 4 z 5, oraz 6 z 7.
W tym wykładzie poznaliśmy (uproszczone) twierdzenie Myhilla-Nerode'a.
Twierdzenie to dostarcza nam jeszcze jednego kryterium do
badania czy języki są regularne -- każdy język regularny ma
skończenie wiele języków ilorazowych.
Jako wniosek z dowodu tego twierdzenia uzyskaliśmy, że istnieje
jeden (z dokładnością do izomorfizmu) minimalny automat
deterministyczny akceptujący dany język.
Poznaliśmy też algorytm wyznaczania tego minimalnego automatu.
- Automat ilorazowy
to minimalny deterministyczny automat skończony
powstały przez sklejenie stanów równoważnych
(zgodnie z daną relacją równoważności na stanach,
spełniającą pewne dodatkowe warunki).
- Algorytm minimalizacji
deterministycznych automatów skończonych --
algorytm wyznaczania minimalnego deterministycznego automatu
skończonego na podstawie dowolnego deterministycznego automatu
skończonego akceptującego dany język.
- Język ilorazowy
języka A, to każdy z języków postaci
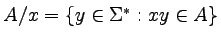 (dla
(dla
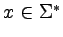 ).
).
Zminimalizuj następujące deterministyczne automaty skończone:
- (4p.)
- (6p.)
Zminimalizuj następujące deterministyczne automaty skończone:
-
Rozwiązanie
-
-
-
Rozwiązanie
-
Rozwiązanie
Możemy skleić stany 1 i 3, oraz 2 i 4.
zamknij
-
Rozwiązanie
Stan 2 nie jest osiągalny i można go pominąć.
zamknij
-
Rozwiązanie
Stan 2 jest nieosiągalny.
Stany 4 i 6 można skleić.
zamknij
-
Rozwiązanie
Stan 6 jest nieosiągalny.
Można skleić stany 1,3 i 4, oraz 2 i 5.
zamknij
-
Rozwiązanie
Stany 2 i 4 są nieosiągalne.
Można skleić stany 3 i 5.
zamknij
-
Rozwiązanie
Stan 2 jest nieosiągalny.
Stany 0 i 4, oraz 1 i 3 można skleić.
zamknij
-
-
-
-
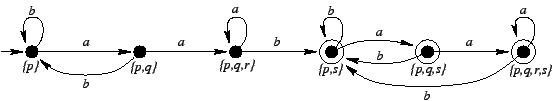

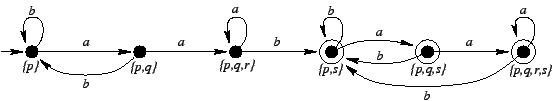

![]() .
Wprost z definicji języka A/x wynika następujący fakt:
.
Wprost z definicji języka A/x wynika następujący fakt:
![]()
![]()
![]()
![]() .
Wynika stąd kolejny fakt:
.
Wynika stąd kolejny fakt:
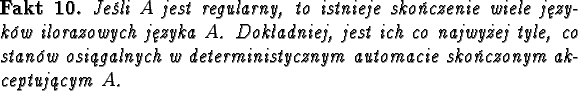
![\begin{theorem}[uproszczone twierdzenie Myhilla-Nerode'a]
Niech $A$ będzie ust...
... skończenie wiele języków ilorazowych
języka $A$.
\end{itemize} \end{theorem}](jfa-main-img481.png)
![]() akceptuje język A.
Niech
akceptuje język A.
Niech
![]() ,
,
![]() .
Zauważmy, że:
.
Zauważmy, że:
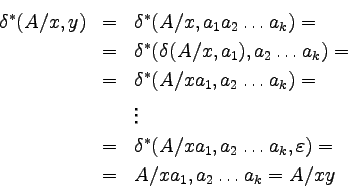
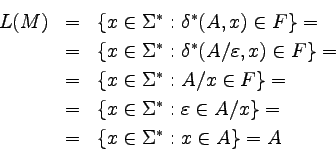
![]() będzie dowolnym ustalonym
deterministycznym automatem skończonym akceptującym język A,
L(M) = A, w którym wszystkie stany są osiągalne.
(Jeśli M zawiera stany nieosiągalne, to najpierw je
usuwamy.)
Każdemu stanowi
będzie dowolnym ustalonym
deterministycznym automatem skończonym akceptującym język A,
L(M) = A, w którym wszystkie stany są osiągalne.
(Jeśli M zawiera stany nieosiągalne, to najpierw je
usuwamy.)
Każdemu stanowi ![]() możemy przypisać język złożony z
tych słów, które prowadzą z q do stanów akceptujących.
Język taki to A/x, gdzie x prowadzi z s do q,
możemy przypisać język złożony z
tych słów, które prowadzą z q do stanów akceptujących.
Język taki to A/x, gdzie x prowadzi z s do q,
![]() .
.
![]() będzie
automatem powstałym z M przez sklejenie ze sobą stanów,
którym przypisaliśmy takie same języki ilorazowe.
Ściśle rzecz biorąc, na stanach automatu M definiujemy
relację równoważności
będzie
automatem powstałym z M przez sklejenie ze sobą stanów,
którym przypisaliśmy takie same języki ilorazowe.
Ściśle rzecz biorąc, na stanach automatu M definiujemy
relację równoważności
![]() określoną w następujący sposób:
określoną w następujący sposób:
![]() jest poprawnie
zdefiniowana.
Musimy w tym celu pokazać, że jeżeli sklejamy ze sobą dwa
stany
jest poprawnie
zdefiniowana.
Musimy w tym celu pokazać, że jeżeli sklejamy ze sobą dwa
stany ![]() ,
, ![]() , to dla dowolnego
, to dla dowolnego ![]() mamy również
mamy również
![]() .
Skoro
.
Skoro ![]() , to A/x = A/y, a zatem
A/xa = A/ya, czyli
, to A/x = A/y, a zatem
A/xa = A/ya, czyli
![]() .
.
![]() akceptuje ten sam język co M,
akceptuje ten sam język co M,
![]() ?
Można pokazać (przez indukcję), że dla dowolnego stanu
?
Można pokazać (przez indukcję), że dla dowolnego stanu
![]() i słowa
i słowa
![]() mamy
mamy
![]() .
Ponieważ jednak nie skleiliśmy żadnego stanu akceptującego z
żadnym ze stanów nieakceptujących, mamy:
.
Ponieważ jednak nie skleiliśmy żadnego stanu akceptującego z
żadnym ze stanów nieakceptujących, mamy: