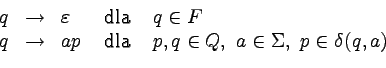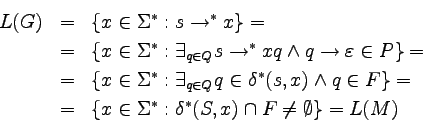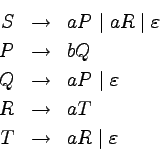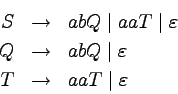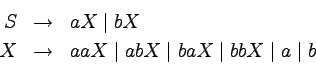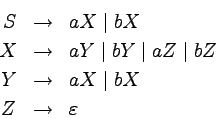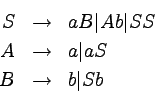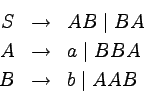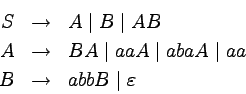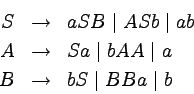W tym wykładzie poznamy gramatyki bezkontekstowe i
opisywaną przez nie klasę języków bezkontekstowych.
Gramatyki bezkontekstowe są formalizmem służącym do opisu
składni -- podobnie jak wyrażenia regularne.
Podobnie również jak wyrażenia regularne są maksymalnie
uproszczonym formalizmem, a wzorce są ich rozbudowaną wersją
przeznaczoną do praktycznych zastosować, tak i gramatyki
bezkontekstowe mają swoją rozbudowaną wersję przeznaczoną do
praktycznych zastosowań.
Są to:
notacja Backusa-Naura
(BNF, ang. Backus-Naur form) oraz
rozszerzona notacja Backusa-Naura
(EBNF, ang. extended Backus-Naur form).
Jest bardzo prawdopodobne, że Czytelnik zetknął się z nimi.
Notacje te są zwykle używane w podręcznikach do ścisłego
opisu składni języków programowania.
Będziemy również badać właściwości klasy języków, które można
opisać gramatykami bezkontekstowymi --
tzw. klasy języków bezkontekstowych.
Jak zobaczymy, siła wyrazu gramatyk bezkontekstowych będzie
większa niż wyrażeń regularnych i automatów skończonych.
Inaczej mówiąc, klasa języków bezkontekstowych zawiera klasę
języków regularnych.
W pierwszym przybliżeniu
BNF
jest formalizmem przypominającym
definicje nazwanych wzorców
ze specyfikacji dla Lex'a.
Główna różnica polega na tym, że zależności między
poszczególnymi nazwami mogą być rekurencyjne.
Specyfikacja w BNF-ie określa składnię szeregu
konstrukcji składniowych, nazywanych też
nieterminalami.
Każda taka konstrukcja składniowa ma swoją nazwę.
Specyfikacja składa się z szeregu reguł
(nazywanych produkcjami), które określają jaką
postać mogą przybierać konstrukcje składniowe.
Nazwy konstrukcji składniowych ujmujemy w trójkątne nawiasy
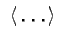 .
Produkcje mają postać:
.
Produkcje mają postać:
<definiowana konstrukcja> ::=
wyrażenie opisujące definiowaną konstrukcję
Wyrażenie opisujące definiowaną konstrukcję może zawierać:
-
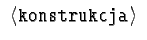 -- nazwy konstrukcji, w tym również
definiowanej, rekurencyjne zależności są dozwolone,
-- nazwy konstrukcji, w tym również
definiowanej, rekurencyjne zależności są dozwolone,
- tekst, ujęty w cudzysłów, który pojawia się dosłownie
w danej konstrukcji,
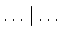 -- oddziela różne alternatywne postaci,
jakie może mieć dana konstrukcja,
-- oddziela różne alternatywne postaci,
jakie może mieć dana konstrukcja,
![$[\dots]$](jfa-main-img154.png) -- fragment ujęty w kwadratowe nawiasy jest opcjonalny.
-- fragment ujęty w kwadratowe nawiasy jest opcjonalny.
Produkcje traktujemy jak możliwe reguły przepisywania --
nazwę konstrukcji stojącej po lewej stronie produkcji możemy
zastąpić dowolnym napisem pasującym do wyrażenia podanego po
prawej stronie.
Każdej konstrukcji składniowej odpowiada pewien język.
Składa sie on z wszystkich tych napisów, które można uzyskać
zaczynając od nazwy konstrukcji i stosując produkcje, aż do
momentu uzyskania napisu, który nie zawiera już żadnych nazw
konstrukcji.
Przykład
BNF może służyć do opisywania składni najrozmaitszych rzeczy.
Oto opis składni adresów pocztowych:
<adres> ::=
<adresat> <adres lokalu>
<adres miasta> <adres kraju>
<adresat> ::=
["W.P." |"Sz.Pan."] <napis> ","
<adres lokalu> ::=
<ulica> <numer> [ "/" <numer> ]
["m" <numer> |"/" <numer> ] ","
<adres miasta> ::=[ <kod> ] <napis>
<adres kraju> ::=[ "," <napis> ]
<kod> ::=
<cyfra> <cyfra> "-" <cyfra> <cyfra> <cyfra>
<cyfra> ::=
"0" |"1" |"2" |"3" |
"4" |"5" |"6" |"7" |
"8" |"9"
<numer> ::= <cyfra> [ <numer> ]
Specyfikacja ta nie jest oczywiście kompletna, gdyż nie
definiuje czym jest napis.
Zwróćmy uwagę na to, że definicja numer jest
rekurencyjna.
Gramatyki bezkontekstowe są uproszczoną wersją notacji BNF.
Konstrukcje składniowe nazywamy tu nieterminalami lub
symbolami nieterminalnymi i
będziemy je oznaczać wielkimi literami alfabetu łacińskiego:
A, B, ..., X, Y, Z.
Wśród nieterminali jest jeden wyróżniony symbol,
nazywany aksjomatem.
To właśnie język związany z tym nieterminalem opisuje gramatyka.
Oprócz nieterminali używamy również terminali
(symboli terminalnych) -- są to znaki stanowiące
alfabet opisywanego przez gramatykę języka.
Będziemy je oznaczać małymi literami alfabetu łacińskiego:
a, b, ....
Produkcje w gramatykach bezkontekstowych mają bardzo prostą
postać: 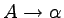 , gdzie A to nieterminal, a
, gdzie A to nieterminal, a 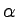 to
słowo, które może zawierać terminale i nieterminale.
Produkcja taka oznacza, że nieterminal A możemy
zastąpić napisem
to
słowo, które może zawierać terminale i nieterminale.
Produkcja taka oznacza, że nieterminal A możemy
zastąpić napisem 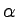 .
Dla jednego nieterminala możemy mieć wiele produkcji.
Oznacza to, że możemy je dowolnie stosować.
Zwykle zamiast pisać:
.
Dla jednego nieterminala możemy mieć wiele produkcji.
Oznacza to, że możemy je dowolnie stosować.
Zwykle zamiast pisać:
Będziemy pisać krócej:
Przykład
Zanim formalnie zdefiniujemy gramatyki bezkontekstowe i
opisywane przez nie języki, spójrzmy na gramatykę opisującą
język:
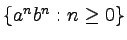
.
Oto sekwencja zastosować produkcji, która prowadzi do
uzyskania słowa aaabbb:
Trzykrotnie stosowaliśmy tutaj produkcję 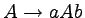 , aby na
koniec zastosować
, aby na
koniec zastosować
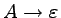 .
.
Definicja
Niech
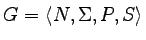
będzie ustaloną gramatyką
bezkontekstową.
Przez
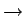
będziemy oznaczać zbiór produkcji
P
traktowany jako relacja,
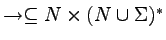
.
Przez
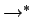
będziemy oznaczać zwrotno-przechodnie domknięcie
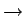
,
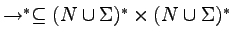
.
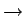 opisuje pojedyncze zastosowanie produkcji, jako
relacja między nieterminalem, a zastępującym go słowem.
Relacje
opisuje pojedyncze zastosowanie produkcji, jako
relacja między nieterminalem, a zastępującym go słowem.
Relacje 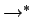 opisuje co można zrobić stosując dowolną liczbę
(łącznie z zero) dowolnych produkcji.
Możemy też przedstawić sobie relację
opisuje co można zrobić stosując dowolną liczbę
(łącznie z zero) dowolnych produkcji.
Możemy też przedstawić sobie relację 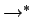 jako skrót do
wielokrotnego iterowania relacji
jako skrót do
wielokrotnego iterowania relacji 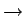 :
:
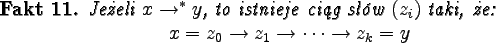
Gramatyka opisuje język złożony z tych wszystkich słów
(nad alfabetem terminalnym), które możemy uzyskać z aksjomatu
stosując produkcje.
Definicja
Niech
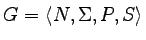
będzie ustaloną gramatyką
bezkontekstową.
Język
generowany (lub
opisywany) przez
gramatykę
G, to:
Alternatywnie, L(G) to zbiór takich słów
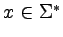 ,
dla których istnieją ciągi słów (zi),
,
dla których istnieją ciągi słów (zi),
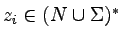 takie, że:
takie, że:
Ciąg (zi) nazywamy wyprowadzeniem słowa x
(w gramatyce G).
Definicja
Powiemy, że język jest bezkontekstowy, jeżeli istnieje
generująca go gramatyka.
Wyprowadzenie stanowi coś w rodzaju dowodu, że dane słowo
faktycznie należy do języka generowanego przez gramatykę.
Istnieje jeszcze inny, bardziej strukturalny, sposób
ilustrowania jak dane słowo można uzyskać w danej gramatyce.
Jest to drzewo wyprowadzenia.
Przyjrzyjmy się zdefiniowanym powyżej pojęciom na przykładach:
Przykład
Weźmy gramatykę generującą język
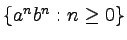
:
Wyprowadzenie słów aaabbb ma postać:
a jego drzewo wyprowadzenia wygląda następująco:
Przykład
Oto gramatyka generująca język palindromów nad alfabetem
{a,b,c}:
Weźmy słowo abbcbba.
Oto jego wyprowadzenie i drzewo wyprowadzenia:
Przykład
Przyjrzyjmy się językowi złożonemu z poprawnych wyrażeń
nawiasowych (dla czytelności zbudowanych z nawiasów kwadratowych).
Język ten możemy zdefiniować na dwa sposoby.
Po pierwsze, wyrażenia nawiasowe, to takie ciągi nawiasów, w których:
- łączna liczba nawiasów otwierających i zamykających jest
taka sama,
- każdy prefiks wyrażenia nawiasowego zawiera przynajmniej
tyle nawiasów otwierających, co zamykających.
Jeżeli zdefiniujemy funkcje
L(x) = #[(x) i
R(x) = #](x), to język wyrażeń nawiasowych możemy
zdefiniować następująco:
Drugi sposób zdefiniowania języka wyrażeń nawiasowych, to
podanie gramatyki bezkontekstowej.
Oznaczmy tę gramatykę przez G.
Oto przykładowe drzewo wyprowadzenia dla wyrażenia nawiasowego
[[][[]]]:
Pokażemy, że obie definicje są sobie równoważne.
W tym celu pokażemy najpierw, że każde słowo, które można
wyprowadzić w G należy do W, a następnie, że
każde słowo z W można wyprowadzić w G.
To, że
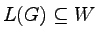 będziemy dowodzić przez indukcję
ze względu na długość wyprowadzenia.
będziemy dowodzić przez indukcję
ze względu na długość wyprowadzenia.
- Jedynym słowem jakie można wyprowadzić w jednym kroku jest
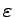 .
Oczywiście
.
Oczywiście
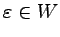 .
.
- Załóżmy, że wyprowadzenie ma postać
![$S \to [S] \to^* [x]$](jfa-main-img580.png) .
Z założenia indukcyjnego x jest wyrażeniem nawiasowym.
W takim razie [x] też, gdyż:
.
Z założenia indukcyjnego x jest wyrażeniem nawiasowym.
W takim razie [x] też, gdyż:
L([x]) = L(x)+1 = R(x)+1 = R([x])
oraz dla każdego prefiksu y słowa x mamy:
- Załóżmy, że wyprowadzenie ma postać:
Z założenia indukcyjnego x i y są wyrażeniami nawiasowymi.
W takim razie xy też, gdyż:
L(xy) = L(x)+L(y) = R(x)+R(y) = R(xy)
oraz dla każdego prefiksu z słowa y mamy:
Z zasady indukcji otrzymujemy
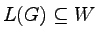 .
.
Pokażemy teraz, że
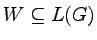 .
Dowód będzie przebiegał przez indukcję po długości słowa.
.
Dowód będzie przebiegał przez indukcję po długości słowa.
- Mamy
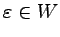 oraz
oraz
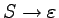 .
.
- Niech
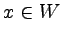 , |x| > 0,
, |x| > 0,
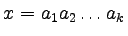 .
Określmy funkcję
.
Określmy funkcję
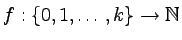 :
:
Zauważmy, że z tego, że x jest wyrażeniem nawiasowym
wynika, że:
f(0) = f(k) = 0
Mamy dwa możliwe przypadki:
- Dla pewnego 0 < i < k mamy f(i) = 0.
Wówczas
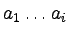 oraz
oraz
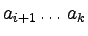 są
wyrażeniami nawiasowymi.
Stąd:
są
wyrażeniami nawiasowymi.
Stąd:
- Dla wszystkich 0 < i < k mamy f(i) > 0.
Wówczas
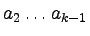 jest wyrażeniem
nawiasowym.
Stąd:
jest wyrażeniem
nawiasowym.
Stąd:
Tak więc 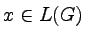 .
.
Na mocy zasady indukcji uzyskujemy
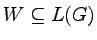 .
Tak więc W = L(G).
.
Tak więc W = L(G).
Często chcemy, aby gramatyka nie tylko opisywała język, ale
również jego strukturę.
Wymagamy wówczas, aby gramatyka była dodatkowo
jednoznaczna.
Definicja
Powiemy, że gramatyka
G jest
jednoznaczna, gdy dla
każdego słowa
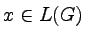
istnieje tylko jedno drzewo
wyprowadzenia słowa
x w gramatyce
G.
Jeśli gramatyka jest jednoznaczna, to drzewa wyprowadzeń
jednoznacznie określają strukturę (składniową) słów z języka.
Nadal oczywiście słowa mogą mieć wiele wyprowadzeń, ale różnią
się one tylko kolejnością stosowanych produkcji, a nie strukturą
wyprowadzania słowa.
Przykład
Oto gramatyka opisująca proste wyrażenia arytmetyczne:
Gramatyka ta jest niestety niejednoznaczna.
Na przykład, wyrażenie 42 + 5 * 2 ma dwa różne drzewa
wyprowadzenia:
Struktura wyrażenia ma wpływ na sposób jego interpretacji.
Drzewo wyprowadzenia po lewej prowadzi do wartości wyrażenia
52, a to po prawej do 94.
Wszędzie tam, gdzie gramatyka opisuje składnię języka, któremu
towarzyszy ściśle zdefiniowana semantyka, będziemy chcieli,
aby była to jednoznaczna gramatyka.
W przypadku wyrażeń arytmetycznych musimy ustalić kolejność
wiązania operatorów, oraz wymusić, aby operatory były albo
lewostronnie, albo prawostronnie łączne.
Oto jednoznaczna gramatyka wyrażeń arytmetycznych:
W tej gramatyce analizowane wyrażenie ma tylko jedno drzewo
wyprowadzenia:
Pokażemy teraz, że wszystkie regularne są bezkontekstowe.
Jak już wcześniej widzieliśmy, odwrotne stwierdzenie nie jest
prawdziwe, gdyż anb n jest językiem bezkontekstowym, ale nie
regularny.
Definicja
Gramatyka (prawostronnie) liniowa, to taka,
w której wszystkie produkcje
mają postać:
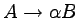
lub
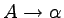
,
dla
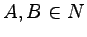
i
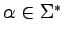
.
Gramatyka silnie (prawostronnie) liniowa, to taka, w której
wszystkie produkcje
mają postać: 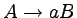 lub
lub
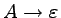 ,
dla
,
dla 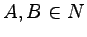 i
i 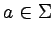 .
.
Okazuje się, że gramatyki liniowe i silnie liniowe opisują
dokładnie klasę języków regularnych.
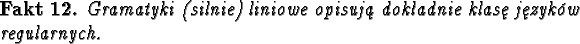
Pokażemy, jak gramatykę liniową przerobić na równoważną jej
gramatykę silnie liniową.
Następnie pokażemy jak można gramatykę silnie liniową
przekształcić na równoważny jej niedeterministyczny automat
skończony i vice versa.
Żeby gramatykę liniową przerobić na silnie liniową, musimy
zastąpić produkcje postaci
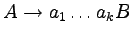 (dla k>1)
oraz produkcje postaci
(dla k>1)
oraz produkcje postaci 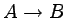 , równoważnymi jej produkcjami
odpowiednimi dla gramatyki silnie liniowej.
, równoważnymi jej produkcjami
odpowiednimi dla gramatyki silnie liniowej.
Jeżeli mamy w gramatyce produkcję postaci 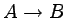 ,
to dla każdej produkcji postaci
,
to dla każdej produkcji postaci 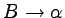 dodajemy
do gramatyki produkcję
dodajemy
do gramatyki produkcję 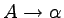 .
Krok ten powtarzamy tak długo, jak długo wprowadza on nowe
produkcje.
Następnie usuwamy wszystkie produkcje postaci
.
Krok ten powtarzamy tak długo, jak długo wprowadza on nowe
produkcje.
Następnie usuwamy wszystkie produkcje postaci 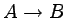 .
W ten sposób uzyskujemy gramatykę generującą ten sam język,
ale nie zawięrającą produkcji postaci
.
W ten sposób uzyskujemy gramatykę generującą ten sam język,
ale nie zawięrającą produkcji postaci 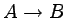 .
.
Dla każdej produkcji postaci:
(dla k>1)
dodajemy do gramatyki nowe terminale
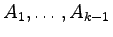 ,
a samą produkcję zastępujemy produkcjami:
,
a samą produkcję zastępujemy produkcjami:
Podobnie, dla każdej
produkcji postaci (dla k>1):
dodajemy do gramatyki nowe terminale
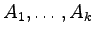 ,
a samą produkcję zastępujemy produkcjami:
,
a samą produkcję zastępujemy produkcjami:
- Gramatykę liniową można sprowadzić do silnie liniowej.
- Gramatykę silnie liniową można przerobić na automat
niedeterministyczny.
- Automat niedeterministyczny można przerobić na gramatykę
silnie liniową.
W rezultacie uzyskujemy gramatykę akceptującą ten sam język,
ale silnie liniową.
Zauważmy, że jeśli gramatyka jest silnie liniowa (lub liniowa), to
w wyprowadzeniu pojawia się na raz tylko jeden nieterminal, i to
zawsze na samym końcu słowa.
Konstruując niedeterministyczny automat skończony równoważny
danej gramatyce silnie liniowej opieramy się na następującej
analogii:
Miech
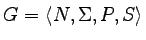 będzie daną gramatyką
silnie liniową.
Stanami automatu będą nieterminale gramatyki N.
Dla każdego słowa
będzie daną gramatyką
silnie liniową.
Stanami automatu będą nieterminale gramatyki N.
Dla każdego słowa
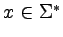 i
i 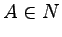 ,
takich, że
,
takich, że 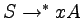 nasz automat po wczytaniu słowa x
będzie mógł przejść do stanu A.
Formalnie konstrukcja naszego automatu M wygląda
następująco
nasz automat po wczytaniu słowa x
będzie mógł przejść do stanu A.
Formalnie konstrukcja naszego automatu M wygląda
następująco
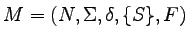 ,
gdzie:
,
gdzie:
oraz:
Można pokazać (przez indukcję po długości słowa), że:
Stąd:
Tak więc faktycznie języki generowane przez gramatyki silnie
liniowe są regularne.
Co więcej, powyższą konstrukcję można odwrócić.
Jeśli
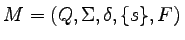 jest danym
niedeterministycznym automatem skończonym (z jednym stanem
początkowym), to równoważna mu gramatyka silnie liniowa ma
postać
jest danym
niedeterministycznym automatem skończonym (z jednym stanem
początkowym), to równoważna mu gramatyka silnie liniowa ma
postać
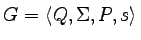 ,
gdzie P zawiera produkcje postaci:
,
gdzie P zawiera produkcje postaci:
Ponownie można pokazać (przez indukcję po długości słowa), że:
Stąd:

Tak więc dla wszystkich języków regularnych istnieją generujące
je gramatyki silnie liniowe.
Tym samym pokazaliśmy, że klasa języków regularnych zawiera się
ściśle w klasie języków bezkontekstowych.
Przykład
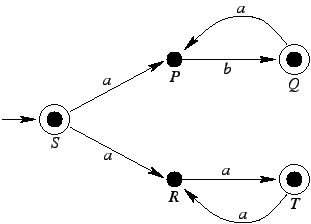
Rozważmy automat skończony akceptujący język
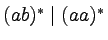
:
Jest on równoważny gramatyce silnie liniowej postaci:
Oto wyprowadzenie przykładowego słowa abab:
Jak widać, odpowiada ono dokładnie obliczeniu automatu
akceptującemu słowo abab.
Jeśli wystarczy nam, aby gramatyka była tylko liniowa, to
wystarczy mniejsza liczba nieterminali:
A oto wyprowadzenie przykładowego słowa abab:
Przykład
Niech
A będzie językiem złożonym ze słów nad alfabetem
{a,b} parzystej długości i różnych od
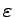
:
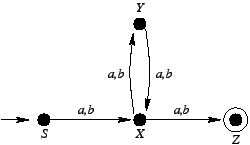
Język ten jest akceptowany przez następujący automat:
Na podstawie tego automatu można stworzyć następującą
gramatykę liniową (ale nie silnie liniową) generującą język A:
Na przykład, słowo abbaaa ma w niej następujące
wyprowadzenie:
Automat ten jest również równoważny następującej
gramatyce silnie liniowej:
Słowo abbaaa ma w tej gramatyce następujące wyprowadzenie:
Jak widać, wyprowadzenie w gramatyce silnie liniowej dokładnie
odpowiada akceptującemu obliczeniu automatu skończonego.
Wyprowadzenie w gramatyce liniowej (ale nie silnie liniowej)
również odpowiada akceptującemu obliczeniu automatu, ale jeden
krok w wyprowadzeniu może odpowiadać kilku krokom automatu.
W tym wykładzie poznaliśmy języki i gramatyki bezkontekstowe
wraz z podstawowymi związanymi z nimi pojęciami.
Pokazaliśmy też, że klasa języków bezkontekstowych zawiera
ściśle w sobie klasę języków regularnych.
- (6p.)
Podaj gramatykę bezkontekstową generującą język
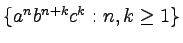 .
Podaj drzewo wyprowadzenia dla słowa aabbbbbccc.
.
Podaj drzewo wyprowadzenia dla słowa aabbbbbccc.
- (4p.)
Podaj liniową gramatykę generująca język
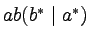 .
.
- Dla gramatyki:
i słowa aabbab:
- podaj jego wyprowadzenie,
- podaj jego drzewo wyprowadzenia,
- czy jest to gramatyka jednoznaczna
(podaj kontrprzykład, lub krótko uzasadnij)?
Rozwiązanie
- Podaj gramatykę bezkontekstową generującą język:
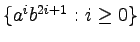 .
Narysuj drzewo wyprowadzenia dla słowa aabbbbb.
Rozwiązanie
.
Narysuj drzewo wyprowadzenia dla słowa aabbbbb.
Rozwiązanie
- Podaj gramatykę bezkontekstową generującą język:
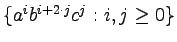 .
Narysuj drzewo wyprowadzenia dla słowa aabbbbbbbbccc.
Rozwiązanie
.
Narysuj drzewo wyprowadzenia dla słowa aabbbbbbbbccc.
Rozwiązanie
- Dla podanej poniżej gramatyki, podaj wyprowadzenie i
drzewo wyprowadzenia słowa baabab.
Czy podana gramatyka jest jednoznaczna
(odpowiedź uzasadnij lub podaj kontrprzykład)?
- Dla podanej poniżej gramatyki, podaj wyprowadzenie i
drzewo wyprowadzenia słowa abbabbaa.
Czy podana gramatyka jest jednoznaczna
(odpowiedź uzasadnij lub podaj kontrprzykład)?
- Dla podanej poniżej gramatyki, podaj wyprowadzenie i
drzewo wyprowadzenia słowa abaabb.
Czy podana gramatyka jest jednoznaczna
(odpowiedź uzasadnij lub podaj kontrprzykład)?
- Podaj gramatykę bezkontekstową generującą język:
-
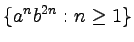 ,
Rozwiązanie
,
Rozwiązanie
-
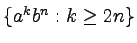 ,
Rozwiązanie
,
Rozwiązanie
-
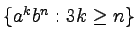 ,
Rozwiązanie
,
Rozwiązanie
-
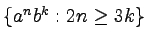 .
.
- {aibjci},
-
{aibjajbi},
-
{aibiajbj},
-
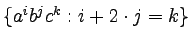 ,
,
-
{aibjck : 3i = 2j+k },
-
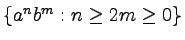 ,
,
-
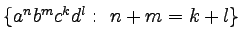 ,
,
-
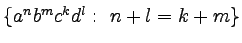 ,
,
-
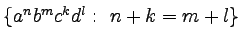 ,
,
-
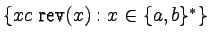 ,
,
-
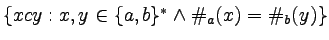 ,
,
-
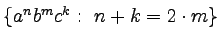 ,
,
- język złożony ze wszystkich słów nad alfabetem {a,b}*, które nie są palindromami.
- Rozszerz podaną w treści wykładu gramatykę wyrażeń arytmetycznych o unarny minus.
Zapewnij aby była jednoznaczna.
Jak silnie powinien wiązać unarny minus?
Jak byś wstawił nawiasy do wyrażenia 3+3*-4*8?
Zdecyduj, czy 2+-4 powinno być poprawnym wyrażeniem.
- Rozszerz gramatykę będącą rozwiązaniem poprzedniego zadania o operację potęgowania (**).
Zapewnij aby była jednoznaczna.
Potęgowanie powinno wiązać mocniej niż mnożenie, ale słabiej niż unarny minus.
Zdecyduj, jak byś wstawił nawiasy do wyrażenia 2**3**4 i tak też zrealizuj gramatykę.
- Podać gramatykę generującą język złożony z takich wyrażeń arytmetycznych składających się z symboli
+,*,0,1,(,), których wartość jest większa niż 2.
- Dla zadanego automatu/wyrażenia regularnego podaj gramatyki
(prawostronnie) liniowe / silnie liniowe opisujące
odpowiedni język:
-
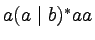 ,
,
-
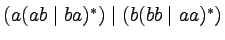 ,
,
-
-
-
-
- Podaj gramatykę wyrażeń regularnych (nad alfabetem {a,b}):
- dowolną,
- jednoznaczną;
- narysuj drzewo wyprowadzenia (w jednoznacznej gramatyce)
dla wyrażenia
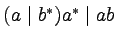 .
.
![]() .
Produkcje mają postać:
.
Produkcje mają postać:
![]() , gdzie A to nieterminal, a
, gdzie A to nieterminal, a ![]() to
słowo, które może zawierać terminale i nieterminale.
Produkcja taka oznacza, że nieterminal A możemy
zastąpić napisem
to
słowo, które może zawierać terminale i nieterminale.
Produkcja taka oznacza, że nieterminal A możemy
zastąpić napisem ![]() .
Dla jednego nieterminala możemy mieć wiele produkcji.
Oznacza to, że możemy je dowolnie stosować.
Zwykle zamiast pisać:
.
Dla jednego nieterminala możemy mieć wiele produkcji.
Oznacza to, że możemy je dowolnie stosować.
Zwykle zamiast pisać:
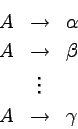
![]() ,
dla których istnieją ciągi słów (zi),
,
dla których istnieją ciągi słów (zi),
![]() takie, że:
takie, że:
![\begin{displaymath}
\xymatrix{
& A \ar@{-}[dl] \ar@{-}[d] \ar@{-}[dr] \\
a &...
...\ar@{-}[dr] & b\\
a & A \ar@{-}[d] & b\\
& \varepsilon
}
\end{displaymath}](jfa-main-img571.png)
![\begin{displaymath}
\xymatrix{
& S \ar@{-}[dl] \ar@{-}[d] \ar@{-}[dr] \\
a &...
...ar@{-}[d] \ar@{-}[dr] & b\\
b & S \ar@{-}[d] & b\\
& c
}
\end{displaymath}](jfa-main-img574.png)
![\begin{displaymath}
\xymatrix{
& & S \ar@{-}[dl] \ar@{-}[d] \ar@{-}[dr] \\
&...
... \varepsilon & [ & S \ar@{-}[d] & ] \\
& & & \varepsilon
}
\end{displaymath}](jfa-main-img577.png)
![]() będziemy dowodzić przez indukcję
ze względu na długość wyprowadzenia.
będziemy dowodzić przez indukcję
ze względu na długość wyprowadzenia.
![\begin{displaymath}
\xymatrix{
S \ar[r] & SS \ar[dl]_>{*} \ar[dr]^>{*} \\
x & & y
}
\end{displaymath}](jfa-main-img582.png)
![]() .
Dowód będzie przebiegał przez indukcję po długości słowa.
.
Dowód będzie przebiegał przez indukcję po długości słowa.
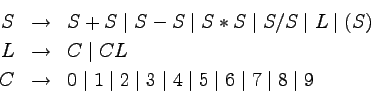
![\begin{displaymath}
\xymatrix{
& & S \ar@{-}[dl] \ar@{-}[d] \ar@{-}[dr] \\
&...
... & & C \ar@{-}[d] & 2 \\
4 & C \ar@{-}[d] & & 5\\
& 2
}
\end{displaymath}](jfa-main-img598.png)
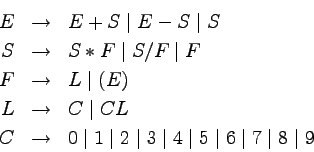
![\begin{displaymath}
\xymatrix{
& & E \ar@{-}[dl] \ar@{-}[d] \ar@{-}[dr] \\
&...
...] & C \ar@{-}[d] & & 2 \\
4 & C \ar@{-}[d] & 5 \\
& 2
}
\end{displaymath}](jfa-main-img600.png)
![]() lub
lub
![]() ,
dla
,
dla ![]() i
i ![]() .
.
![]()
![]() (dla k>1)
oraz produkcje postaci
(dla k>1)
oraz produkcje postaci ![]() , równoważnymi jej produkcjami
odpowiednimi dla gramatyki silnie liniowej.
, równoważnymi jej produkcjami
odpowiednimi dla gramatyki silnie liniowej.
![]() ,
to dla każdej produkcji postaci
,
to dla każdej produkcji postaci ![]() dodajemy
do gramatyki produkcję
dodajemy
do gramatyki produkcję ![]() .
Krok ten powtarzamy tak długo, jak długo wprowadza on nowe
produkcje.
Następnie usuwamy wszystkie produkcje postaci
.
Krok ten powtarzamy tak długo, jak długo wprowadza on nowe
produkcje.
Następnie usuwamy wszystkie produkcje postaci ![]() .
W ten sposób uzyskujemy gramatykę generującą ten sam język,
ale nie zawięrającą produkcji postaci
.
W ten sposób uzyskujemy gramatykę generującą ten sam język,
ale nie zawięrającą produkcji postaci ![]() .
.
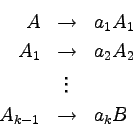
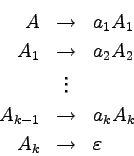
![]() będzie daną gramatyką
silnie liniową.
Stanami automatu będą nieterminale gramatyki N.
Dla każdego słowa
będzie daną gramatyką
silnie liniową.
Stanami automatu będą nieterminale gramatyki N.
Dla każdego słowa
![]() i
i ![]() ,
takich, że
,
takich, że ![]() nasz automat po wczytaniu słowa x
będzie mógł przejść do stanu A.
Formalnie konstrukcja naszego automatu M wygląda
następująco
nasz automat po wczytaniu słowa x
będzie mógł przejść do stanu A.
Formalnie konstrukcja naszego automatu M wygląda
następująco
![]() ,
gdzie:
,
gdzie:
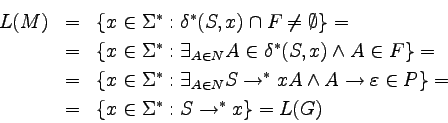
![]() jest danym
niedeterministycznym automatem skończonym (z jednym stanem
początkowym), to równoważna mu gramatyka silnie liniowa ma
postać
jest danym
niedeterministycznym automatem skończonym (z jednym stanem
początkowym), to równoważna mu gramatyka silnie liniowa ma
postać
![]() ,
gdzie P zawiera produkcje postaci:
,
gdzie P zawiera produkcje postaci: