Wykład poświęcony będzie metodom tworzenia sieci neuronowych, a w szczególności metodzie wstecznej propagacji.
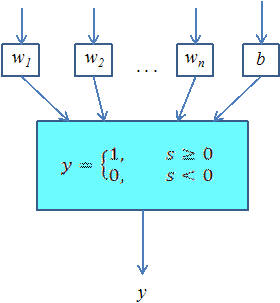
Perceptronem nazywamy prosty element obliczeniowy, który sumuje ważone sygnały wejściowe i proównuje tę sumę z progiem aktywacji - w zależności od wyniku perceptron może być albo wzbudzony (wynik 1), albo nie (wynik 0). Na poprzednim wykładzie mogliśmy się przekonać, że użycie perceptronu jako klasyfikatora jest możliwe, jednak jego możliwości są ograniczone do zbiorów separowalnych liniowo. W praktyce jednak możemy spróbować wykorzystać perceptron również wtedy, gdy zbiory nie są separowalne liniowo - godząc się na pewną (możliwie małą) liczbę błędnych rozpoznań.

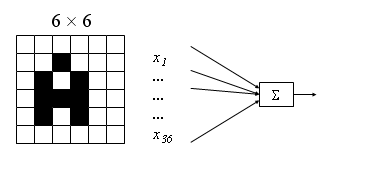
Przykład: rozważmy prosty problem rozpoznawania litery A na rysunku. Załóżmy dla uproszczenia, że czarno-biały rysunek ma rozdzielczość 6x6 punktów. Do kazdego z tych punktów podłączymy jedno wejście naszego perceptronu, a więc będzie miał on 36 wejść (i tyle samo wag). Wyjście: 1, jeśli na wejściu pojawia się litera "A", zaś 0 w przeciwnym przypadku. Nie potrafimy z góry przewidzieć, jak będą wyglądały wszystkie możliwe litery "A", chcielibyśmy zamiast tego podać perceptronowi możliwie dużo przykładów (różnych liter) i zaznaczyć, które z nich ma rozpoznawać jako "A".
Możemy do tego użyć algorytmu uczenia perceptronu - tzn. automatycznego doboru wag na podstawie napływajacych przykładów. W uproszczonym (ze względu na ilustrację) przypadku dwuwymiarowym algorytm wygląda następująco:
w1 += n * (d-y) * x1
w2 += n * (d-y) * x2
b +=
n * (d-y)
gdzie n jest niewielkim współczynnikiem uczenia (n > 0), d - oczekiwana odpowiedź a y - odpowiedź neuronu.
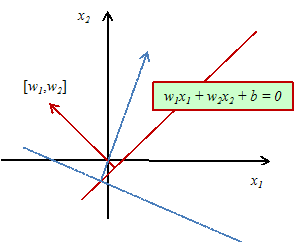
Po wyczerpaniu przykładów zaczynamy proces uczenia od początku, dopóki następują jakiekolwiek zmiany wag połączeń. Warto zwrócić uwagę na graficzną interpretację powyższych wzorów. Każdy źle zaklasyfikowany przypadek powoduje przechylenie prostej oddzielającej pozytywne odpowiedzi perceptronu od negatywnych w kierunku zmierzającym do przerzucenia wadliwego przykładu na drugą stronę prostej.
Opisany schemat jest w miarę przejrzysty tylko dla pojedynczych perceptronów lub niewielkich sieci. Ciężko jest stosować reguły tego typu dla bardziej skomplikowanych modeli. Tymczasem np. do rozpoznawania wszystkich liter potrzeba by sieci złożonej z 26 takich perceptronów, a żeby wyniki rozpoznawania były satysfakcjonujące, powinniśmy użyć wielowarstwowej sieci neuronowej.
Ograniczenia pojedynczych perceptronów spowodowały w latach 80-tych wzrost zainteresowania sieciami wielowarstwowymi i opracowanie algorytmu ich uczenia (propagacja wsteczna). Okazuje się, że już stosunkowo prosta architektura polegajaca na tym, że tworzymy kilka (zwykle 3) warstw neuronów połączonych w ten sposób, że wyjścia neuronów należących do warstwy niższej połączone są z wejściami neuronów należących do warstwy wyższej (każdy z każdym), pozwala na tworzenie sieci o niemal dowolnej charakterystyce. Działanie takiej sieci polega na liczeniu odpowiedzi neuronów w kolejnych warstwach - najpierw w pierwszej, do której trafiają sygnały z wejść sieci, potem (na podstawie wyników pierwszej warstwy) liczymy odpowiedzi drugiej warstwy neuronów itd., przy czym odpowiedzi ostatniej warstwy traktowane są jako wyjścia z sieci.
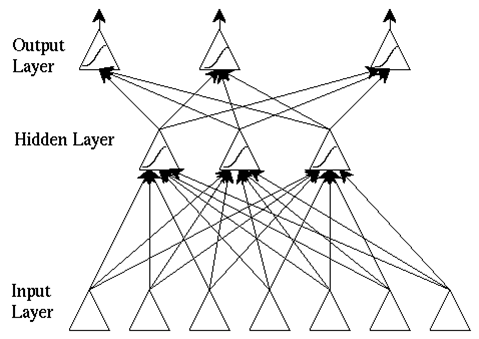
Nie jest znana ogólna metoda projektowania optymalnej architektury sieci neuronowej dla zadanego problemu. W praktyce zwykle wykorzystuje się sieci podobne do powyzszej.
Aby sieć wielowarstwowa mogła wykorzystać swe atuty (w szczególności trenować wagi algorytmem propagacji wstecznej), funkcja aktywacji neuronów nie powinna być skokowa. W praktyce wykorzystuje się kilka rodzajów funkcji aktywacji, dbając jedynie, by była ona monotoniczna, różniczkowalna (jak się przekonamy, to cecha ważna podczas trenowania sieci) i z wyglądu przypominała "rozmyty schodek". Na potrzeby niniejszego wykładu przyjmijmy, że funkcja aktywacji będzie sigmoidalna - poniżej przedstawiono własności i przykładowe wykresy tej funkcji (dla różnych wartości dodatkowego parametru):
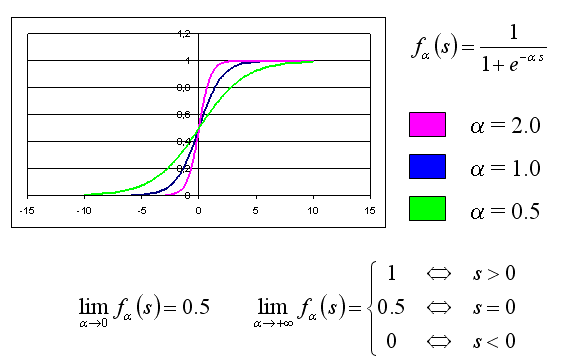
Ogólny wzór na wartość wyjściową neuronu przedstawia się następująco:
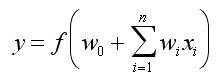
gdzie w0 jest dodatkową wagą pełniącą rolę analogiczną do progu aktywacji w perceptronie.
Przy ustalonych (np. wytrenowanych) wagach sieć neuronowa może być traktowana jako pewna funkcja rzeczywista n zmiennych (gdzie n jest liczbą wejść sieci; załóżmy, że sieć ma tylko jedno wyjście). Możemy się zastanawiać, pamiętając o ograniczeniu dotyczącym perceptronu, jakie rodzaje funkcji może taka sieć neuronowa przybliżać. Okazuje się, że odpowiedź jest dość optymistyczna:
(Z tw. Kołmogorowa): Sieci wielowarstwowe (minimum 3 warstwy) potrafią modelować, tzn. dowolnie dokładnie przybliżać, dowolne ciągłe funkcje rzeczywiste o wartościach z odcinka [0,1].
Powyższy wynik oznacza, że dla większości problemów praktycznych polegajacych na aproksymacji (przewidywaniu) wartości funkcji istnieje taka sieć neuronowa, która jest dowolnie dokładnym rozwiązaniem problemu. Niestety, twierdzenie to nic nie mówi o praktycznych sposobach szukania takiej sieci - pozostają nam metody przybliżone w rodzaju opisanej poniżej metody wstecznej propagacji.
Przekonajmy się, jak wygląda wykres funkcji danej przez prostą sieć neuronową (odcienie szarości na wykresie odpowiadają wartościom na wyjściu, osie - zmiennym wejściowym):
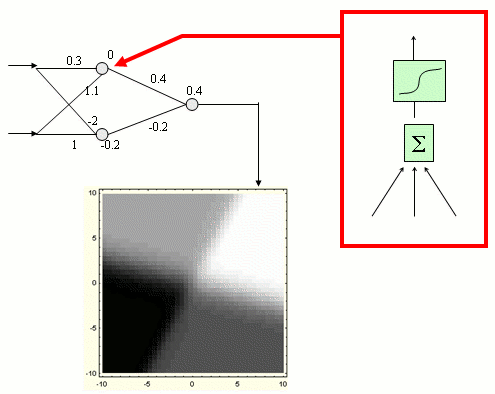
Sieć trochę bardziej skomplikowana:
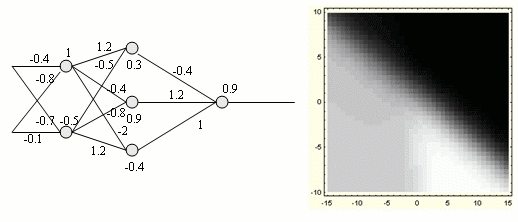
W razie potrzeby moglibyśmy nawet podać jawny wzór funkcji odpowiadającej sieci neuronowej, choć byłby on całkowicie nieczytelny w przypadku większej liczby neuronów. Oto przykład dla trzech neuronów w dwóch warstwach ("zerowa" warstwa to tylko wejście do sieci):
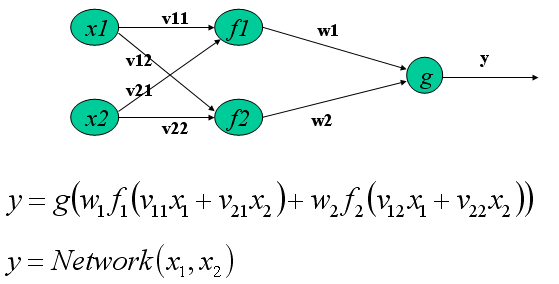
Łatwo zauważyć, że gdyby wszystkie poszczególne funkcje aktywacji były liniowe, to funkcja Network, jako ich złożenie będzie również liniowa. A funkcję liniową możemy zamodelować pojedynczym liniowym neuronem - oznacza to, że architektura wielowarstwowa daje nowe możliwości tylko w przypadku stosowania nieliniowych funkcji aktywacji.
Podobnie jak w przypadku pojedynczego neuronu, główną zaletą sieci neuronowej jest to, że nie musimy "ręcznie" dobierać wag. Możemy te wagi wytrenować, czyli znaleźć ich w przybliżeniu optymalny zestaw za pomocą metody obliczeniowej zwanej wsteczną propagacją błędu. Jest to metoda umożliwiająca modyfikację wag w sieci o architekturze warstwowej (opisanej w poprzednim rozdziale), we wszystkich jej warstwach.
Ogólny schemat procesu trenowania sieci wygląda następująco:
Aby znależć taki zestaw wag, dla którego błąd sieci jest jak najmniejszy, możemy zapisać ten błąd jako funkcję od wartości wag. Oznaczmy przez:
f: R -> R – funkcję aktywacji w neuronie
w1 ,..., wK – wagi połączeń wchodzących
z1 ,..., zK – sygnały napływające do neuronu z poprzedniej warstwy.
Zwykle błąd liczony jest jako kwadrat odchylenia: d = 1/2 (y-t)2, co możemy rozpisać jako:
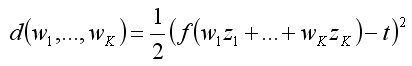
W celu ustalenia, o ile powinna zmienić się waga neuronu, powiniśmy "rozłożyć" otrzymany błąd całkowity na połączenia wprowadzające sygnały do danego neuronu. Składową błędu dla każdego j-tego połączenia określamy jako pochodną cząstkową błędu względem j-tej wagi. Poniższe przykłady ilustrują zasadność takiego podejścia.
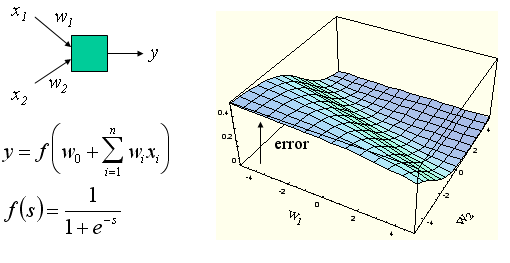
Załóżmy, że mamy neuron z wagami w0=0, w1=2, w2=3. Mamy dany wektor wejściowy: [0.3 , 0.7], przy czym oczekiwana odpowiedź to t=1. Jak należy zmienić wagi, aby błąd był jak najmniejszy? Narysujmy wykres wartości błędu w zależności od wag:
Jeśli rozważymy większą liczbę przykładów, funkcja średniego błędu będzie miała bardziej skomplikowany kształt. Np. dla zbioru danych:
[0.3, 0.7], t=1
[0.2, 0.9], t=0.1
[-0.6, 1], t=0
[0, -0.8], t=0.5
[0.6, 1], t=0.3
średni błąd w funkcji wag wygląda następująco:
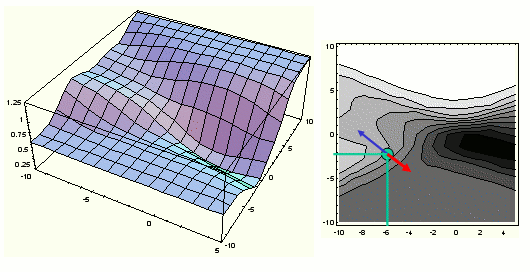
Oczywiście zależy nam na znalezieniu takich wag, dla których średni błąd jest najmniejszy. Nie możemy w tym celu sprawdzić wszystkich kolejnych wartości wag, zamiast tego zastosujemy metodę niewielkich kroków (zmian wag) we właściwym kierunku (czyli w kierunku, w którym błąd spada). Nachylenie wykresu w punkcie odpowiadającym aktualnym wartościom wag, dane jest przez gradient, czyli wektor pochodnych cząstkowych (niebieska strzałka). Zmiana wag powinna nastąpić w kierunku przeciwnym (czerwona strzałka).
Wzór ogólny na gradient błędu w funkcji wag można wyprowadzić nastepująco:
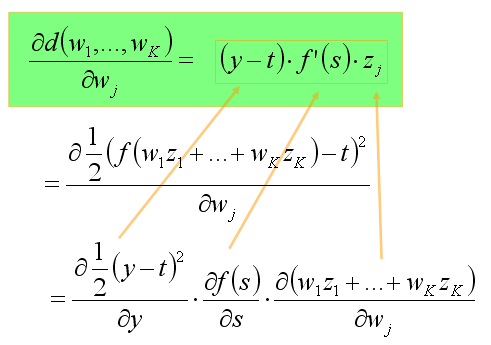
Wektor wag połączeń powinniśmy przesunąć w kierunku przeciwnym do wektora gradientu błędu (z pewnym współczynnikiem uczenia q). Możemy to zrobić po każdym przykładzie uczącym albo sumując zmiany po kilku przykładach. Uwzględniając powyższe wyprowadzenie, wzór na zmianę konkretnej wagi wygląda nastepująco:
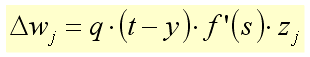
Powyższe wyprowadzenie jest prawidłowe tylko dla ostatniej warstwy, kiedy wiemy, jaka powinna być prawidłowa wartość wyjścia (wówczas możemy policzyć błąd). Dla wcześniejszych warstw takiej informacji bezpośrednio nie mamy. Zamiast tego błąd ten będziemy przybliżać, przenosząc go (propagując) z kolejnych warstw. Oznaczmy: w - waga wejścia neuronu, z - sygnał wchodzący do neuronu danym wejściem, d - współczynnik błędu obliczony dla danego neuronu, s - wartość wzbudzenia (suma wartości wejściowych pomnożonych przez wagi) dla danego neuronu. Pomocniczy współczynnik błędu d zdefiniujemy dla ostatniej warstwy jako:
a dla pozostałych warstw:

czyli neuron w warstwie ukrytej "zbiera" błędy di z neuronów, z którymi jest połączony. Zmiana wag połączeń następuje jednocześnie we wszystkich warstwach, po fazie propagacji błędu (tak, aby wszelkie obliczenia na wszystkich warstwach odbywały się jeszcze na starych wartościach wag) i odbywa się według wzoru:
Wzór ten jest uogólnieniem wzoru wyprowadzonego wcześniej dla ostatniej warstwy.
Opisany powyżej proces propagacji błędu powtarzany jest dla każdego przypadku uczącego (lub kilku przypadków uśrednionych). Jest to proces dość kosztowny obliczeniowo - jeśli sieć jest rozbudowana (a nierzadko sieci miewają kilkaset neuronów) i przypadków uczących jest dużo (np. kilkaset tysięcy, przy czym zwykle nie wystarczy raz przejść przez wszystkie), cały proces może zająć godziny lub dni. Jest to jednak proces jednorazowy: wytrenowana sieć neuronowa może zostać "zamrożona" i działać już tylko jako klasyfikator, bez dalszego uczenia (a więc szybko).
Głównym tematem wykładu były algorytmy uczenia sieci neuronowych - poczynając od prostej reguły uczenia perceptronu, na algorytmie wstecznej propagacji błędu skończywszy. Podane informacje powinny już wystarczyć do implementacji prostej sieci neuronowej i wytrenowania jej.
Zalecana literatura:
Szczegółowe definicje znajdują się w treści wykładu (słowa kluczowe zaznaczone są na czerwono).
algorytm wstecznej propagacji błędu - metoda uczenia sieci wielowarstwowej, w której błąd ostatniej warstwy jest przesyłany wstecz i wykorzystywany do zmiany wartości wag w poprzednich warstwach.
dane treningowe - znane przykłady, na podstawie których próbujemy znaleźć zasadę ogólną
neuron - według konwencji przyjetej na tym wykładzie, perceptron daje w wyniku 0 lub 1, a neuron - dowolną liczbę z przedziału [0,1] (dzięki np. sigmoidalnej funkcji aktywacji)
perceptron - prosty model naturalnego neuronu, jego działanie polega na ważonym sumowaniu sygnałów wejściowych i nieliniowym (np. progowym) przekształceniu ich w wartość wyjściową
sieć wielowarstwowa - sieć połączonych neuronów, w której neurony przesyłają sygnały wszystkim neuronom kolejnej warstwy (połączenie między warstwami: każdy z każdym)
wagi połączeń - parametry perceptronu, przez które mnożymy wartość sygnałów wejściowych
wartość progowa - parametr perceptronu wyznaczający granicę, powyżej której perceptron jest wzbudzony (tzn. ma na wyjściu wartość 1)
3.1. Zaimplementować prosty algorytm uczenia perceptronu i sprawdzić jego działanie na zbiorze danych (może być sztuczny).