Definicja
Wartością średnią w próbce (lub średnią próbkową, średnią próbki), oznaczaną symbolem 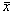 , nazywamy wielkość
, nazywamy wielkość
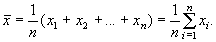
| « poprzedni punkt |
Wskaźniki sumaryczne są charakterystykami (parametrami) liczbowymi obliczonymi dla analizowanych danych.
Wskaźniki położenia (lub miary położenia, parametry położenia) charakteryzują wielkości najbardziej reprezentatywne dla danych, centralną "tendencję" danych, określają "centrum" lub "środek" próbki. Najważniejsze wskaźniki położenia obliczane dla próbki to: wartość średnia, mediana, moda, średnia ucięta i średnia winsorowska.
Niech x1, x2, ... ,xn będzie próbką, gdzie n jest licznością (rozmiarem) próbki.
Definicja
Wartością średnią w próbce (lub średnią próbkową, średnią próbki), oznaczaną symbolem 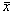 , nazywamy wielkość
, nazywamy wielkość
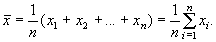
Wartość średnia próbki jest średnią arytmetyczną wszystkich elementów próbki.
Niech x(1), x(2), ... , x(n-1), x(n) będą ustawionymi w kolejności niemalejącej elementami próbki, więc x(1) jest najmniejszą, x(n) jest największą obserwacją w próbce, oraz
x(1) £
x(2) £
... £
x(n−1) £
x(n).
Definicja
Medianą w próbce (lub medianą próbki, medianą próbkową), oznaczaną symbolem xmed, nazywamy wielkość
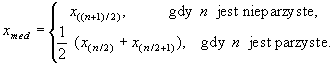
Przykład
Wiek 25-ciu pracowników zgrupowano w przedziałach:
|
Przedział (klasa) |
Obserwacje | Liczność | Częstość |
| [18,23) | 20 | 1 | 1/25 = 0,04 |
| [23,28) | 24, 27, 25 | 3 | 3/25 = 0,12 |
| [28,33) | 30, 30, 31, 32, 29, 28 | 6 | 6/25 = 0,24 |
| [33,38) | 33, 35, 37, 36, 35, 37, 36 | 7 | 7/25 = 0,28 |
| [38,43) | 39, 40, 38, 41 | 4 | 4/25 = 0,16 |
| [43,48) | 43, 45, 46 | 3 | 3/25 = 0,12 |
| [48,53) | 49 | 1 | 1/25 = 0,04 |
Obliczymy wartości poznanych wskaźników położenia.
Średnia wieku pracowników wynosi
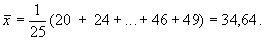
Rozmiar próbki n=25, zatem (n+1)/2=13. Mediana wieku pracowników jest 13-tą co do wielkości obserwacją równą x(13)=35.
Czasem dysponujemy obserwacjami od razu zgrupowanymi (zagregowanymi). Wówczas wartość średnią obliczamy na podstawie histogramu. Jest to:
(suma liczności przedziałów pomnożonych przez środki przedziałów)/liczność próbki.
W przykładzie
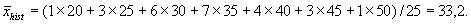
Oczywiście, wartość średnia obliczona na podstawie histogramu z reguły różni się nieco od wartości średniej obliczonej na podstawie dokładnych wartości.
Przykład
Miesięczne dochody 11-tu osób wynoszą (w zł.): 2000 dla czterech osób, 2500 dla czterech osób, 3500 dla dwu osób, oraz 19000. Średnie wynagrodzenie tej grupy osób to:
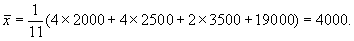
Dochody badanych osób uporządkujemy rosnąco:
x(1) = x(2) = x(3) = x(4) = 2000
x(5) = x(6) = x(7) = x(8) = 2500
x(9) = x(10) = 3500, x(11) = 19000.
Zauważmy, że
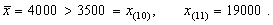
Zatem 10 osób spośród 11-tu ma dochód mniejszy od obliczonego średniego dochodu. Średni dochód pracowników nie odzwierciedla "typowego" dochodu dla analizowanych danych. Mówimy, że średnia jest wrażliwa na obserwacje odstające (tzn. znacznie mniejsze lub znacznie większe od większości obserwacji).
Lepszą miarą przeciętnego wynagrodzenia jest mediana: xmed = x(6)=2500, która jest odporna (mało wrażliwa) na obserwacje odstające.
Średnia ucinana jest stosowana wówczas, gdy pewien procent (liczba) najmniejszych oraz największych wartości w próbce jest (może być) wynikiem błędu, np. w przypadku błędnego przetworzenia danych lub błędów przyrządów pomiarowych.
Ostrzeżenie: obserwacje odstające mogą być czasem bardzo istotne, np. gdy są wynikiem rozregulowania procesu produkcji.
Średnia ucinana może być lepszym parametrem położenia niż mediana, która jest niestabilna przy małej liczności próby i znacznie różniących się kolejnych obserwacjach.
Pytanie kontrolne
Oblicz średnią próbkową, średnią ucinaną oraz medianę dla danych z przedostatniego przykładu po dodaniu 2 obserwacji: 31 i 32 (lata).
Zobacz odpowiedź
Średnią winsorowską stosujemy wówczas, gdy wartości skrajne (k najmniejszych i k największych) są niepewne, co do ich prawdziwych wartości lub gdy zostały utracone z bazy danych, lub też nie mogły być zaobserwowane (np. w przypadku badania czasu życia, czasu bezawaryjnej pracy urządzenia gdy eksperymentator ma ograniczony czas obserwowania zjawiska).
Ostrzeżenie: interpretując dane na podstawie miar położenia nie można zapomnieć o analizie histogramu, np. w przypadku symetrycznego, dwumodalnego histogramu mogą one nie odzwierciedlać centrum danych.
Wskaźniki rozproszenia (lub miary rozproszenia, parametry rozproszenia) charakteryzują rozrzut danych, rozproszenie wartości próbki wokół parametru położenia.
Rozstęp informuje nas jedynie o długości najmniejszego przedziału zawierającego wszystkie elementy próbki (zwanego nośnikiem), tracimy informację o obserwacjach odstających, kształcie rozkładu cechy w próbce (np. czy histogram jest symetryczny, spłaszczony, wyostrzony, ...).
Definicja
Odchyleniem standardowym w próbce ( próbki), oznaczanym przez s, nazywamy pierwiastek z wariancji w próbce:
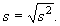
Odchylenie standardowe jest wyrażone w tych samych jednostkach, co obserwacje w próbce.
Kwadraty odchyleń w definicji wariancji powodują zwiększony (zmniejszony) wpływ na nią większych (mniejszych) odchyleń od średniej.
Zauważmy, że w powyższym wskaźniku rozproszenia udział odchylenia każdej obserwacji od średniej jest proporcjonalny do wielkości odchylenia, a nie jego kwadratu jak w przypadku wariancji.
Uwagi
Dolnym (pierwszym) kwartylem, oznaczanym przez Q1, nazywamy medianę podpróbki składającej się z "połowy" najmniejszych elementów próbki, tzn. wszystkich elementów próbki uporządkowanych niemalejąco, które poprzedzają medianę.
Górnym (trzecim) kwartylem, oznaczanym przez Q3, nazywamy medianę podpróbki składającej się z "połowy" największych elementów próbki, tzn. wszystkich elementów próbki uporządkowanych niemalejąco, które występują po medianie.
Medianę nazywamy czasem drugim kwartylem i oznaczamy przez Q2.
Wykres ramkowy ( pudełkowy) ilustruje wzajemne położenie pięciu wskaźników sumarycznych:
x(1) = xmin, Q1, xmed, Q3, x(n) = xmax.
Poniższy rysunek 1.16 przedstawia przykładowy wykres ramkowy.
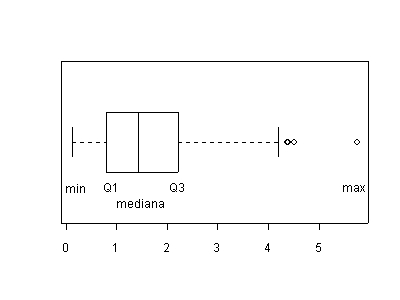
Rys. 1.16. Wykres ramkowy.
Z wykresu odczytujemy następujące wskaźniki:
Zatem długość podstawy prostokąta to rozstęp międzykwartylowy IQR. W przykładzie IQR» 0,6.
Linie po obu stronach prostokąta nazywamy wąsami wykresu ramkowego. Rzutem lewego wąsa na oś poziomą jest przedział [x* ,Q1], a rzutem prawego wąsa jest przedział [Q3,x* ], gdzie
x* = min {xi : Q1 - 1,5 ´ IQR £ xi £ Q1, i=1,...,n },
x* = max {xi : Q3 £ xi £ Q3 + 1,5 ´ IQR, i=1,...,n }.
Obserwacje, które są mniejsze niż Q1- 1,5´ IQR lub większe niż Q3+ 1,5´ IQR uważane są za potencjalne obserwacje odstające. Na wykresie ramkowym są to rzuty na oś poziomą środków małych kwadracików (lub kółeczek). Na rysunku 1.16 widzimy jedną taką obserwację, równą w przybliżeniu 1,6.
Uwaga
Wąsy mogą mieć długość co najwyżej 1,5´
IQR. Obserwacje większe od Q3+
1,5´
IQR lub mniejsze od
Na podstawie rys. 1.16 stwierdzamy, że obserwacje w próbce są bardziej rozproszone na prawo od wartości średniej niż na lewo od niej. 50% największych obserwacji jest w przedziale [0,3, 1,6], natomiast 50% najmniejszych w przedziale [0,1, 0,3].
| « poprzedni punkt |