Twierdzenie (o całkowaniu przez części)
Jeżeli funkcje u i v mają na pewnym przedziale P ciągłe pochodne u' i v', to
na tym przedziale.
| « poprzedni punkt | następny punkt » |
Niestety, nie każdą funkcję da się przedstawić jako sumę prostych do scałkowania składników. Musimy wówczas korzystać z innych metod. Ich podstawą są dwa twierdzenia. Pierwsze nosi nazwę twierdzenia o całkowaniu przez części i jest konsekwencją wzoru na różniczkowanie iloczynu funkcji.
Twierdzenie (o całkowaniu przez części)
Jeżeli funkcje u i v mają na pewnym przedziale P ciągłe pochodne u' i v', to
na tym przedziale.
Dowód
Zapiszmy wzór na różniczkowanie iloczynu funkcji
| [u(x)v(x)]' = u'(x)v(x) + u(x)v'(x) |
w postaci
| u(x)v'(x) = [u(x)v(x)]' - u'(x)v(x). |
Całkując go obustronnie dostajemy
czyli istotnie
Wykorzystanie twierdzenia oraz powszechnie stosowaną w procesie obliczeniowym notację ilustruje poniższy przykład.
Przykład
![]()
Metodę całkowania przez części stosujemy do całkowania iloczynów pewnych funkcji. Należy jednak podkreślić, że nie każdą całkę iloczynu funkcji obliczamy w ten sposób. W omawianej metodzie obliczenie interesującej nas całki zastępujemy obliczeniem innej całki - występującej po prawej stronie równości. Takie postępowanie ma sens tylko wówczas, gdy całka po prawej stronie równości jest łatwiejsza do wyznaczenia.
Mimo ograniczeń metody, wiele ważnych całek iloczynów dwóch funkcji oblicza się w ten sposób. W szczególności, ponieważ każda funkcja f może być zapisana jako iloczyn 1× f, przy jej użyciu wyznaczamy m. i. całkę funkcji logarytmicznej.
Przykład
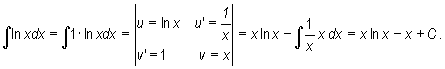
W podobny sposób wyznaczamy też całki funkcji cyklometrycznych.
Metodę całkowania przez części stosujemy z powodzeniem w następujących sytuacjach:
Przykład
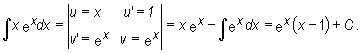
Przykład
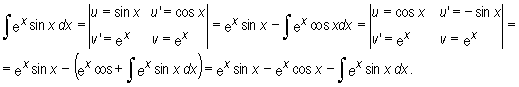
Przenosząc ostatnią całkę na lewą stronę i dzieląc przez 2 otrzymujemy
![]()
Uwaga
Przy wyznaczaniu powyższej całki przyjęcie u = ex, v' = sinx jest również poprawne.
Przykład
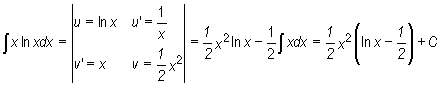
Dodajmy, że metoda całkowania przez części pozwala efektywnie wyznaczać tzw. wzory rekurencyjne, które określają związek między całkami zależnymi od kolejnych liczb naturalnych.
Drugie twierdzenie - o całkowaniu przez podstawienie (zwane również twierdzeniem o zamianie zmiennych) - jest konsekwencją reguły różniczkowania funkcji złożonej (superpozycji funkcji).
Twierdzenie (o całkowaniu przez podstawienie)
Jeżeli funkcja f jest całkowalna na przedziale P, zaś funkcja g ma ciągłą pochodną na przedziale T i przekształca go na przedział P oraz znana jest całka
to
Dowód
Niech F będzie funkcją pierwotną funkcji f. Z przyjętych założeń funkcja złożona F ° g jest różniczkowalna i zgodnie z twierdzeniem o różniczkowaniu funkcji złożonej ( Wykład 4)
| (F(g(x))' = F'(g(x)) g'(x) = f(g(x)) g'(x). |
Zatem
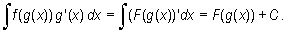 |
Powszechnie stosowaną konwencję zapisu obliczeń wg tej metody ilustruje poniższy przykład.
Przykład
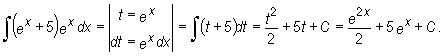
Po dokonaniu wyboru podstawienia t = g(x) = ex, obliczamy różniczkę dt nowej zmiennej t przez obustronne różniczkowanie równości t = ex . Następnie wyznaczamy całkę funkcji zmiennej t. Po jej obliczeniu wracamy do wyjściowej zmiennej niezależnej.
Przykład
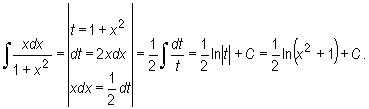
W oparciu o powyższe twierdzenie łatwo jest uzasadnić dwa często wykorzystywane wzory.
Stwierdzenie
Jeżeli f jest całkowalna, zaś F jest jej funkcją pierwotną, to
Pytanie kontrolne 8.3
Wykorzystując podstawienie t = ax+b podaj dowód powyższego stwierdzenia.
Zobacz odpowiedźPrzykład
![]()
Stwierdzenie
Jeżeli funkcja f jest różna od zera i różniczkowalna na pewnym przedziale P, to
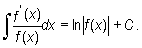 |
Czyli "całka nieoznaczona ułamka, którego licznik jest pochodną mianownika, równa się logarytmowi wartości bezwzględnej mianownika".
Pytanie kontrolne 8.4
Podaj dowód powyższego stwierdzenia wykorzystując podstawienie t= f(x).
Zobacz odpowiedźPrzykład
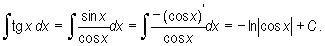
Pytanie kontrolne 8.5
Wyznacz całkę
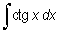 .
.
Istotą prezentowanej metody jest zastąpienie oryginalnej funkcji podcałkowej funkcją, której całkę nieoznaczoną potrafimy wyznaczać. Nie zawsze stosowane podstawienia są tak "naturalne" jak przedstawionych przykładach. Niektóre wymagają sporego doświadczenia i inwencji.
Nie ma niestety uniwersalnej reguły pozwalającej na wybór właściwego podstawienia - w licznych przypadkach możliwe jest natomiast otrzymanie rozwiązania dla różnych podstawień.
Przykład
Całkę ![]() obliczymy trzema sposobami.
obliczymy trzema sposobami.
Sposób I. Podstawienie t = sin x
![]()
Sposób II. Podstawienie t = cos x
![]()
Sposób III.
![]()
Uwaga
Przez proste przekształcenia trygonometryczne można wykazać, że występujące w rozwiązaniach funkcje pierwotne różnią się jedynie o stałą wartość (wykazać!).
Istnieje wszakże szereg ważnych klas funkcji, dla których znane są podstawienia gwarantujące uzyskanie rozwiązań. Poniżej zaprezentujemy najważniejsze z nich.
| « poprzedni punkt | następny punkt » |