| « poprzedni punkt | następny punkt » |
Algorytm sortowania, który zamierzamy omówić w tym punkcie jest algorytmem rekurencyjnym, wykorzystującym zasadę "dziel i zwyciężaj", tak jak to było w przypadku algorytmu QuickSort. Teraz jednak nasze postępowanie będzie zupełnie inne. Zamiast operacji rozdzielania ciągu, stosujemy operację scalania już uporządkowanych fragmentów ciągu. Omawiany algorytm nosi nazwę MergeSort.
Idea algorytmu sortowania przez scalanie
Z przedstawionej idei algorytmu wynika, że etap początkowy polega na kolejnych podziałach ciągu na części. Na tym etapie nie wykonujemy żadnych porównań, ani zmian w ciągu danych. Dopiero, gdy dojdziemy do ciągów jednoelementowych, możemy zacząć scalanie.
Przykład 5.1
Rozważmy ciąg 5,7,4,9,3,6,2,1. Potraktujmy, każdy z elementów tego ciągu jako jednoelementowy uporządkowany ciąg. Zastosujemy procedurę scalania do sąsiadujących ciągów, otrzymując 4 dwuelementowe posortowane ciągi: {5,7}, {4,9}, {3,6}, {1,2}. Teraz ponownie zastosujemy scalanie sąsiednich ciągów tworząc dwa czteroelementowe segmenty uporządkowane {4,5,7,9}, {1,2,3,6}. Wykonanie jeszcze jednego scalania pozwoli nam utworzyć ciąg uporządkowany {1, 2, 3, 4, 5, 6, 7, 9}.J
Na rysunku 4.2 przedstawiono graf rekurencyjnych wywołań funkcji MergeSort.
Operacja, którą wykonywać będziemy wielokrotnie w omawianym algorytmie sortowania, to scalanie. Ponieważ scalanie dotyczy tu sąsiadujących fragmentów jednego ciągu, a wynik scalania powinien być też zapisany w tym samym ciągu, zmodyfikujemy nieco algorytm Merge przedstawiony w poprzednim punkcie.
Niech Scal(l,x,p) będzie procedurą, która realizuje scalanie dwóch odcinków danego ciągu e, wyznaczonych przez indeksy l, x, oraz x+1, p. Oczywiście zakładamy, że l £ x £ p. W pierwszym kroku algorytmu przepiszemy elementy e[l],...,e[x] oraz e[x+1],...,e[p] do dwóch tablic pomocniczych a i b. Następnie powtórzymy postępowanie z algorytmu Merge zapisując ciąg wyjściowy na pozycjach e[l],...,e[p]. Procedura scalania przyjmie teraz postać.
|
Scal |
(l,x,p: :int ) |
|
{ |
n := x-l+1; m := p-x; |
|
for i := 1 to n do a[i] := e[l+i-1] od; |
|
|
for i := 1 to m do b[i] := e[x+i] od; |
|
|
a[n+1] := + ¥; b[m+1]:= + ¥; |
|
|
i := 1; j := 1; k := l; |
|
|
while (k £ p) do |
|
|
|
if (a[i] £ b[j]) then |
|
e[k] := a[i]; i := i+1 |
|
|
|
else |
|
|
e[k] := b[j]; j := j+1 |
|
fi; |
|
|
|
k := k+1 |
|
od; |
|
|
} |
Korzystając z analizy poprawności algorytmu Merge, możemy udowodnić następujące twierdzenie.
Twierdzenie 5.1 Jeżeli {e[l]£ ...£ e[x], e[x+1]£ ...£ e[p] oraz e[i] = ei dla i= l,...,p}, to po wykonaniu procedury Scal(l,x,p) w dowolnej strukturze danych z porządkiem liniowym, spełniony jest warunek
e[l]£ ...£ e[p] oraz ciąg e[l],...,e[p] jest permutacją elementów ciągu el ,..., ep.
Algorytm
Algorytm sortowania przez scalanie można zapisać bardzo elegancko jako rekurencyjną procedurę MergeSort o dwóch parametrach l, p, będących indeksami lewego i prawego końca rozważanej części ciągu. Oczywiście w celu posortowania tablicy e[1],...,e[n] należy wywołać tę procedurę z parametrami 1, n.
| MergeSort (l, p : int){ | |||
| if (l < p) | |||
| x :=(l+p) div 2; | // l £ x £ p | ||
| MergeSort(l, x); | // e[l] £ ...£ e[x-1] £ e[x] | ||
| MergeSort(x+1, p); | // e[x+1] £ ... £ e[p-1] £ e[p] | ||
| Scal(l, x, p); | // e[1] £...£ e[x] £e[x+1] £ ... £ e[p-1] £ e[p] | ||
| fi; | |||
| } | |||
Przykład 5.2
Przyjrzyjmy się dokładniej, jak wygląda proces dzielenia ciągu na fragmenty i jak te fragmenty są następnie scalane w kolejnych etapach algorytmu. W poniższej tabeli zaznaczono tylko numery pozycji rozdzielanych i następnie scalanych dla ciągu o szesnastu elementach.
| 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 | |||||||||||||||
| 1,2,3,4,5,6,7,8 | 9,10,11,12,13,14,15,16 | ||||||||||||||
| 1,2,3,4 | 5,6,7,8 | 9,10,11,12 | 13,14,15,16 | ||||||||||||
| 1,2 | 3,4 | 5,6 | 7,8 | 9,10 | 11,12 | 13,14 | 15,16 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1,2 | 3,4 | 5,6 | 7,8 | 9,10 | 11,12 | 13,14 | 15,16 | ||||||||
| 1,2,3,4 | 5,6,7,8 | 9,10,11,12 | 13,14,15,16 | ||||||||||||
| 1,2,3,4,5,6,7,8 | 9,10,11,12,13,14,15,16 | ||||||||||||||
| 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 | |||||||||||||||
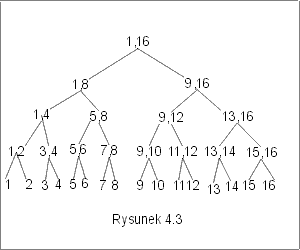
Na rysunku 4.3 przedstawiono drzewo rekurencyjnych wywołań procedury MergeSort dla n=16. Idąc w dół tego drzewa dokonujemy podziału każdego zadania na dwa podzadania. Następnie wracając, scalamy odpowiadające fragmenty ciągu.

Poprawność algorytmu:
Dowód poprawności algorytmu przeprowadzimy przez indukcję ze względu na długość sortowanego ciągu. Jeżeli l = p to ciąg zawiera tylko jeden element i jest uporządkowany. Procedura MergeSort nie wykona w tym przypadku żadnych porównań. Rozważmy wykonanie algorytmu MergeSort dla ciągu e[l],... ,e[p], gdzie l< p i załóżmy, że procedura MergeSort sortuje poprawnie dowolny ciąg o długości mniejszej. Skoro l < p, to zostanie wykonana instrukcja warunkowa, będąca treścią procedury MergeSort. Ponieważ x = (l+p) div 2, więc (x - l) < (p - l) oraz p-(x+1) < (p - l). Oba ciągi e[l], ..., e[x] oraz e[x+1], ..., e[p] są krótsze od ciągu e[l],... ,e[p]. Na mocy założenia indukcyjnego, po wykonaniu instrukcji "MergeSort(l,x);" otrzymamy
e[l] £ ...£ e[x-1] £ e[x],
a po wykonaniu "MergeSort(x+1,p);"
e[x+1] £ ... £ e[p-1] £ e[p].
Na mocy twierdzenia o poprawności procedury Scal, po wykonaniu instrukcji "Scal(l,x,p)" cały rozważany ciąg jest posortowany:
e[l] £...£ e[x] £e[x+1] £ ... £ e[p-1] £ e[p].
Wynika stąd, że dla dowolnego ciągu algorytm wykonuje poprawnie zadanie sortowania.
Twierdzenie 5.2 Algorytm MergeSort jest całkowicie poprawnym rozwiązaniem problemu sortowania, w każdej strukturze danych z liniowym porządkiem £.
Koszt algorytmu:
Niech T(n) będzie liczbą porównań wykonanych przez algorytm MergeSort dla ciągu o n elementach. Załóżmy dla wygody, że n jest potęgą dwójki, np. n= 2k. Ponieważ scalenie dwóch ciągów o długości n/2 wymaga n porównań, zatem mamy następujące równanie rekurencyjne, opisujące koszt algorytmu MergeSort
T(1) = 0, T(2k) = 2 T(2 k-1) + n.
Rozwiązaniem tego równania jest funkcja T(n) = Q(n lg n). Koszt algorytmu MergeSort mierzony liczbą wykonanych porównań elementów ciągu jest liniowo-logarytmiczny ze względu na rozmiar danych. Bardziej wnikliwa analiza scalania pokazuje, że algorytm MergeSort wymaga Q(n lg n) porównań, zarówno w przypadku najlepszym, jak i w przypadku pesymistycznym.
Uwaga.
1. Algorytm MergeSort nadaje się doskonale do zrównoleglenia: wywołania rekurencyjne mogą
być przecież realizowane przez dwa różne procesory.
2. Przyglądając się bliżej algorytmowi MergeSort dojdziemy do wniosku, że
etapy algorytmu związane z dzieleniem zadania na podzadania możemy pominąć.
Możemy zacząć od razu od scalania, łącząc najpierw elementy w pary
uporządkowane, potem w czwórki itd. Taka realizacja algorytmu nie wymaga
użycia rekursji. Niestety struktura algorytmu jest wtedy bardziej skomplikowana.
Dokładne zapisanie tego algorytmu pozostawiamy Czytelnikowi jako
ćwiczenie.
Pytanie 5: Ile razy zostanie wykonana instrukcja "x:= (l+p)/2", jeżeli algorytm MergeSort zastosowano do ciągu n elementowego, a n jest potęgą dwójki?
| « poprzedni punkt | następny punkt » |