| « poprzedni punkt | następny punkt » |
Problem
Dany jest ciąg macierzy A1, A2,...,An. Obliczyć iloczyn A1 ´ A2 ´ ... ´ An, tak by koszt wykonania zadania był najmniejszy.
Wiadomo, że dwie macierze możemy pomnożyć tylko wtedy, gdy liczba kolumn w pierwszej z nich jest taka sama, jak liczba wierszy w drugiej. W powyższym problemie zakładać będziemy, że wymiary macierzy są odpowiednie, aby ich pomnożenie było możliwe.
Niech p0, p1,... pn oznacza ciąg, w którym para (pi-1, pi) jest rozmiarem macierzy Ai (macierz Ai ma więc pi-1 wierszy i pi kolumn). Przy takim założeniu obliczenie iloczynu możemy wykonać po kolei mnożąc A1 przez A2, następnie wynik przez A3 itd, albo mnożąc najpierw macierze z jakiegoś wybranego segmentu np. od Ai do Aj, a potem obliczając iloczyn A1 ´... ´ Ai-1 ´ W ´ Aj+1´... ´ An, gdzie W = Ai ´ Ai+1 ´ ... ´ Aj. Oczywiście pamiętamy, że mnożenie macierzy nie jest przemienne, jest natomiast łączne i z tej własności będziemy właśnie korzystać szukając optymalnego rozwiązania problemu.
Przykład 2.1
Niech A, B i C będą macierzami o wymiarach odpowiednio (10 ´ 100), (100 ´ 5) i (5 ´ 50). Iloczyn tych macierzy możemy obliczyć albo licząc najpierw iloczyn A ´ B a potem mnożąc wynik przez C, albo najpierw licząc B ´ C, a potem mnożąc A przez otrzymany wynik. Macierze uzyskane w wyniku są oczywiście identyczne
(A ´ B) ´ C = A ´ (B ´ C).
Obliczmy liczbę wykonanych mnożeń skalarnych w obu przypadkach pamiętając, że pomnożenie macierzy o wymiarach (n ´ m) przez macierz o wymiarach (m ´ k) wymaga m* n * k mnożeń elementów tych macierzy, jeśli używamy zwykłego algorytmu opartego na algebraicznej definicji mnożenia macierzy.
Dla wyrażenia (A ´ B) ´ C mamy więc (10*100*5) + (10 *5 * 50) mnożeń, bo w wyniku pomnożenia A przez B otrzymamy macierz o wymiarze (10 ´ 5). Wykonany więc 7500 mnożeń skalarnych.
Dla wyrażenia A ´ (B ´ C) mamy (10*100*50) + (100 * 5 * 50) mnożeń, bo w wyniku mnożenia B przez C otrzymamy macierz o wymiarach (100 ´ 50). Tym razem wykonamy 75000 mnożeń skalarnych. Różnica jest istotna! J
Najprostszy pomysł rozwiązania problemu mnożenia łańcucha macierzy przedstawia następujący algorytm.
Algorytm naiwny
1. Rozważyć wszystkie możliwe ustawienia nawiasów w ciągu.
2. Dla każdego ustawienia nawiasów wyliczyć koszt mnożenia.
3. Wybrać to ustawienie nawiasów, przy którym koszt liczony liczbą wykonanych mnożeń jest najmniejszy.
4. Obliczyć iloczyn macierzy dla wybranego ustawienia nawiasów.
Taki algorytm gwarantuje, że liczba wykonanych mnożeń skalarnych (wykonujemy je tylko w punkcie czwartym tego algorytmu) jest minimalna. Punkty 1-3 powyższej metody mają charakter pomocniczy. Przy ich realizacji wykonujemy jednak pewną liczbę mnożeń i dodawań liczb naturalnych. Zastanówmy się jaki jest koszt z tym związany. Pytanie właściwie dotyczy liczby przypadków, które trzeba rozważyć, gdyż punkt drugi wymaga co najwyżej O(n) mnożeń rzeczywistych dla łańcucha złożonego z n macierzy. Ile jest więc możliwych ustawień nawiasów w ciągu złożonym z n macierzy?
Oznaczmy przez P(n) liczbę ustawień nawiasów w ciągu n elementowym. Przyjmijmy, że dla n=1, P(1)=1. Dla n=2 mamy tylko jedno ustawienie nawiasów, a dla n=3, dwa ustawienia, tak jak w przykładzie 2.1. Ogólnie, jeśli pierwszy nawias postawimy po pozycji ktej rozdzielając ciąg mnożeń na dwa podciągi A1 ´ A2 ´ ... ´ Ak i Ak+1 ´ Ak+2 ´ ... ´ An, to liczba ustawień nawiasów w tym przypadku wynosi P(k)*P(n-k). Ponieważ k może przyjąć dowolną z wartości od 1 do n-1, więc otrzymujemy następujący wzór rekurencyjny:
P(1) = 1, P(n) = S k=1 ,...,n-1 P(k)*P(n-k) dla n>1 (*)
Zauważmy, że P(4) = 5, P(5) = 14, a P(6) = 42. Funkcja ta dość szybko rośnie. I rzeczywiście
Lemat 2.1 Rozwiązaniem równania rekurencyjnego (*) jest (n-1)sza liczba Catalana,
P(n)= c(n-1), gdzie c(n) = (2n nad n)/(n+1).
Formuła Stirlinga (n! ~ sqrt(2np) nn/en) pozwala przybliżyć liczbę Catalana następująco:
c(n) ~ 4n*n-3/2/sqrt(p).
Wynika stąd, że liczba możliwych ustawień nawiasów w ciągu n macierzy jest wykładnicza. Nawet dla niewielkich wartości n, taki algorytm byłby zbyt kosztowny. Musimy więc szukać innego rozwiązania.
Lemat 2.2 Problem mnożenia łańcucha macierzy ma własność optymalnej podstruktury.
Nazwijmy optymalnym nawiasowaniem ciągu A1, A2,...,An taki układ nawiasów, dla którego koszt pomnożenia wszystkich macierzy, mierzony liczbą mnożeń skalarnych, jest najmniejszy. Niech będzie optymalne nawiasowanie ciągu A1, A2,...,An, w którym został on rozbity na dwa podciągi A1 ´ A2 ´ ... ´ Ak i Ak+1 ´ Ak+2 ´ ... ´ An,
A1 ´ A2 ´ ... ´ An = (A1 ´ A2 ´ ... ´ Ak ) ´ ( Ak+1 ´ Ak+2 ´ ... ´ An).
Układ nawiasów musi być optymalny zarówno w ciągu A1 ´ A2 ´ ... ´ Ak, jak i w ciągu Ak+1 ´ Ak+2 ´ ... ´ An, gdyż w przeciwnym razie moglibyśmy rozważyć inne nawiasowanie całego ciągu, dające mniejszy koszt mnożenia macierzy, niż to, w tej chwili rozważane. Czyli optymalne rozwiązanie problemu mieści w sobie optymalne rozwiązania dla podproblemów. Ten fakt zachęca do zastosowania metody programowania dynamicznego.
Zajmijmy się teraz policzeniem kosztu rozwiązania optymalnego. Niech m(i,j) będzie minimalną liczbą mnożeń skalarnych potrzebnych do policzenia iloczynu Ai ´ A2 ´ ... ´ Aj dla i £ j. Mamy m(i,i) = 0, oraz dla i<j
m(i,j) = min {m(i,k) + m(k+1, j) + pi-1*pk*pj : i £ k < j}. (**)
W minimum po prawej stronie równości (**), k zmienia się od i do j-1, co odpowiada ustawieniu pierwszego nawiasu po pozycji ktej. W wyniku mnożenia macierzy Ai ´ Ai+1 ´ ... ´ Ak otrzymamy macierz o wymiarach pi-1´ pk, a w wyniku mnożenia macierzy Ak+1 ´ Ak+2 ´ ... ´ Aj macierz o wymiarach pk´ pj . Koszt pomnożenia tych macierzy wynosi więc pi-1*pk*pj. Jeśli k wybierzemy tak, by wartość m(i,k) + m(k+1,j) + pi-1*pk*pj była najmniejsza, to koszt pomnożenia Ai ´ Ai+1 ´ ... ´ Aj jest najmniejszy z możliwych. Oznaczmy tę wybraną wartość k przez s(i,j).
Może się wydawać, że obliczenie wartości m(i,j) możemy powierzyć procedurze rekurencyjnej. Gdybyśmy użyli wprost wzoru (**) do policzenia wartości m(i,j), to musielibyśmy wywoływać rekurencyjnie tę procedurę dla podproblemów (i,k) i (k+1,j), dla wszystkich k od i do j. To jednak w konsekwencji doprowadziłoby do dalszych rekurencyjnych wywołań, przy czym wiele ze spotkanych podproblemów powtarzałoby się.
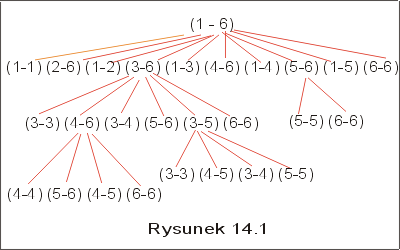
Na rysunku 14.1 przedstawiliśmy fragment drzewa możliwych rekurencyjnych wywołań przy obliczaniu m(1,6). Drzewo to ma dwa typy wierzchołków: wierzchołki z etykietami i-j, odpowiadające wywołaniu rekurencyjnemu funkcji m(i,j), oraz wierzchołki oznaczone pojedynczą liczbą, wskazującą podział aktualnego zadania na dwa podzadania. Zauważmy, że w wielu wierzchołkach występują te same wskaźniki. Oznacza to ponowne wykonanie tego samego rekurencyjnego obliczenia.
 |
Pytanie 2: Jaki byłby koszt algorytmu rekurencyjnego obliczania wszystkich wartości m(i,j)?
Rzeczywiście, obliczenie wartości m(1,n) moglibyśmy oszacować za pomocą funkcji rekurencyjnej T(n), takiej że T(1) ³1, T(n) ³ (1+ Sk=1,...,n-1(T(k) + T(n-k) + 1) dla n>1. Zakładamy, że na wykonanie instrukcji początkowych oraz porównania przy wyborze minimum potrzebujemy jednostkę czasu. Łatwo sprawdzić, że musi być T(n) ³ 2n-1, tzn . rozwiązaniem jest funkcja rosnąca co najmniej tak szybko jak 2n-1. A więc koszt obliczenia wartości m(1,n) byłby wykładniczy.
Wyciągnijmy jednak z tych rozważań wniosek pozytywny: skoro podproblemy, które musimy rozważać powtarzają się, nasz problem ma własność wspólnych podproblemów. Jeszcze jeden sygnał, że być może metoda programowania dynamicznego da dobre rezultaty. Zamiast więc powtarzać obliczenia wielokrotnie dla tych samych podproblemów, zapamiętajmy wcześniej wyliczone wartości w tablicy.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Kłopot polega teraz tylko na ustaleniu, w jakim porządku wyliczać wielkości m(i,j). Zauważmy, że przy obliczaniu m(i,j) korzystamy we wzorze (**) z wartości m(i,i), m(i,i+1),...,m(i,j-1) oraz z wartości m(i+1,j), m(i+2,j),..., m(j,j). Są to elementy i-tego wiersza i j-tej kolumny. Wynika stąd, że wyliczenie m(i,j) powinniśmy wykonywać wzdłuż diagonali, zgodnie z numeracją przedstawioną na rysunku 14.2 Otrzymujemy stąd następujący algorytm:
Algorytm MM
| { | |
|
| for i := 1 to n do m(i,i) := 0; | //inicjalizacja diagonali | |
| for l :=2 to n do | // l= numer diagonali | |
| for i := 1 to n-l+1 do | //kolejne pozycje l-tej diagonali | |
| j := i + l - 1 ; | |
|
| m(i,j) := +¥ ; | |
|
| for k := i to j-1 do | //szukamy najlepszego podziału | |
| q := m(i,k) + m(k+1,j) + pi-1*pk *pj; | ||
| if q< m(i,j) then m(i,j) := q; s(i,j):= k fi | //s(i,j) zapamiętujemy indeks, przy którym osiągnięto minimum | |
| od | ||
| od | ||
| od | ||
| } | |
|
Koszt algorytmu
W algorytmie występują trzy zagnieżdżone pętle. Każda z nich wykonuje się rzędu O(n) razy, zatem koszt czasowy algorytmu można oszacować przez O(n3). Koszt pamięciowy natomiast jest kwadratowy O(n2) i związany jest z koniecznością zapamiętania wartości m(i,j) oraz s(i,j).
Przykład 2.2
Przypuśćmy, że mamy sześć macierzy A1 (4 ´ 2), A2 (2´ 3), A3 (3 ´ 1), A4 (1 ´ 2),A5 (2 ´ 2), A6 (2 ´ 3) i chcemy obliczyć iloczyn A1 ´ A2 ´ ... ´ A6. Obliczmy zgodnie z algorytmem MM minimalną liczbę mnożeń skalarnych, którą trzeba wykonać przy obliczaniu tego iloczynu. W tabeli na rysunku 14.3 przedstawiliśmy wartości m(i,j), a wartości najlepszych podziałów w tablicy s. Na przykład do policzenia m(2,5) potrzebujemy wartości:
m(2,2) + m(3,5) + 2*3*2 = 0 + 10 + 12 = 22,
m(2,3) + m(4,5) + 2*1*2 = 6 + 4 + 4 = 14,
m(2,4) + m(5,5) + 2*2*2 = 10 + 0 + 8 = 18.
Najmniejsza wartość to 14 i dlatego m(2,5) = 14. Ponieważ została ona osiągnięta, gdy k=3 (tzn. nawias postawiono po trzeciej macierzy) więc s(2,5)= 3. Optymalne ustawienie nawiasów w tym przykładzie wygląda następująco :
A1 ´ A2 ´ ... ´ A6= (A1 ´ (A2 ´ A3)) ´ ((A4 ´ A5) ´ A6).
Najmniejsza liczba mnożeń skalarnych to w tym przykładzie 36.J
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mając wszystkie wartości s(i,j) dla i<j możemy wypisać optymalne nawiasowanie. Następujący rekurencyjny algorytm "wypisz" odczytuje z tablicy s pozycje, w których mają być umieszczone nawiasy w optymalnym nawiasowaniu.
| wypisz( i,j : int){ | |
|
| if (i = j) then | ||
| write (i) | // wypisujemy numer macierzy, która ma w tym miejscu występować. | |
| else | ||
| if (i < j) then | ||
| write("("); | |
|
| wypisz (i, s(i,j)); | //wypisz optymalne ustawienie nawiasów w ciągu i,...,s(i,j) | |
| write("´"); | |
|
| wypisz(s(i,j)+1, j); | //wypisz optymalne ustawienie nawiasów w ciągu s(i,j)+1,...,j | |
| write(")"); | |
|
| fi; | ||
| fi } | |
|
Koszt procedury wypisz jest liniowy ze względu na liczbę mnożonych macierzy.
Skoro umiemy wypisać optymalny układ nawiasów, to możemy tę wiedzę wykorzystać, wykonując w odpowiedniej kolejności mnożenie macierzy. Algorytm wyliczania iloczynu łańcucha macierzy, korzystający z tablicy najlepszego nawiasowania s przedstawiono jako rekurencyjną funkcję mult. Zakładamy, że dany jest łańcuch macierzy A1, A2, ..., An, dla którego wyliczono wcześniej najlepsze nawiasowanie zapamiętane w tablicy s(i,j). Wynikiem tej funkcji jest iloczyn A1 ´ A2 ´ ... ´ An, a liczba mnożeń użyta do wyliczenia tego iloczynu jest najmniejsza z możliwych.
| mult( i,j : int){ | ||
| if (i < j) then | |
|
| X := mult (i, s(i,j) ); | |
|
| Y := mult (s(i,j)+1, j) | |
|
| return X ´ Y; | |
|
| else | |
|
| return Ai | ||
| fi; | |
|
| } | |
|
Pytanie 3: Rozważmy macierze A1 (4 ´ 2), A2 (2´ 300), A3 (300 ´ 1), A4 (1 ´ 2),A5 (2 ´ 2), A6 (2 ´ 300). Jaka jest minimalna liczba mnożeń skalarnych potrzebna do obliczenia iloczynu A1 ´ A2 ´ ... ´ A6?
| « poprzedni punkt | następny punkt » |