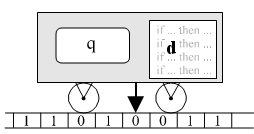
Działanie maszyny:- Startujemy z pewnego miejsca na taśmie i ze stanu sterowania q0.
- Czytamy symbol s z taśmy.
- Na podstawie tych dwóch danych (stan q = q0, symbol s) za pomocą funkcji d obliczamy:
Poprzedni wykład był poświęcony przybliżonym metodom radzenia sobie z trudnymi problemami optymalizacyjnymi. Ten wykład koncentruje się na próbie zdefiniowania, co to znaczy, że problem jest trudny.
Zaprezentowane na poprzednim wykładzie algorytmy heurystyczne dają zwykle (w bardziej skomplikowanych przypadkach) rozwiązania przybliżone. Dlaczego godzimy się na rozwiązania niedokładne, skoro - jak wiemy - każdy problem optymalizacyjny można rozwiązać dokładnie przez przegląd przestrzeni stanów? Odpowiedzią na to pytanie jest wysoka złożoność obliczeniowa takiego rozwiązania.
Przypomnijmy kilka podstawowych pojęć:
Złożoność czasowa - liczba "podstawowych operacji", jakie musi wykonać dany algorytm rozwiązujący zadanie.
Złożoność pamięciowa - liczba "podstawowych jednostek pamięci", które zajmuje program podczas pracy.
Złożoność jest funkcją wielkości problemu, a więc gdy mówimy np. o złożoności kwadratowej, mamy na myśli konieczność wykonania rzędu n2 kroków, gdzie n to wielkość danych wejściowych. (Uwaga: oznacza to, że np. złożoność algorytmu rozkładającego liczbę n na czynniki pierwsze nie liczy się względem n, tylko log(n), gdyż taki jest rozmiar w bitach liczby n)
Złożoność obliczeniową można szacować jako złożoność pesymistyczną (dla najgorszych możliwych danych), lub średnią (dla danych "losowych"). Tak rozumiana złożoność jest cechą algorytmu, a nie problemu; można jednak czasem udowodnić, że dany problem nie może zostać rozwiązany algorytmem o zbyt niskiej złożoności. Takie sytuacje są dla nas szczególnie interesujące, wskazują bowiem na konieczność wykorzystywania metod przybliżonych.
Czasem, jak np. w przypadku problemu sortowania, nawet mimo dużej przestrzeni stanów (n!) jesteśmy w stanie podać efektywne metody rozwiązania. Są jednak problemy o statusie niepewnym: jedyne znane algorytmy mają złożoność wykładniczą (np. 2n, a więc o wiele za dużo, nawet dla niewielkich danych wejściowych), a przy tym nikt jeszcze nie udowodnił, że nie istnieją prostsze metody. Zadania takie będziemy zaliczać do "trudnych".
Przykłady - zadania "łatwe"
We wszystkich tych przypadkach znamy efektywne algorytmy dające dokładne rozwiązania.
Przykłady - zadania "trudne"
We wszystkich tych przypadkach znane algorytmy dokładne mają wysoką (wykładniczą) złożoność czasową. Musimy szukać metod przybliżonych.
Dalsza analiza problemów złożoności obliczeniowej wymaga wykorzystania pewnego modelu obliczeń, jakim jest maszyna Turinga.
Deterministyczna Maszyna Turinga (DTM) to piątka {Q, S, d, q0, F}, gdzie:
Q - zbiór stanów sterowania maszyny,
S - alfabet (zbiór symboli) taśmy,
d - funkcja przejścia:
Działanie maszyny:
- Startujemy z pewnego miejsca na taśmie i ze stanu sterowania q0.
- Czytamy symbol s z taśmy.
- Na podstawie tych dwóch danych (stan q = q0, symbol s) za pomocą funkcji d obliczamy:
Mimo prostoty sformułowania maszyna Turinga dysponuje bardzo dużymi możliwościami obliczeniowymi. Jest przy tym na tyle ściśle zdefiniowana, że można z jej pomocą dokładnie określić, jaka jest złożoność czasowa danego algorytmu - jest to dokładnie liczba pojedynczych kroków maszyny. To nas uniezależnia od takich drobiazgów technicznych, jak zastanawianie się nad konkretnym rodzajem procesora i efektami kompilacji programu (w celu ścisłego policzenia liczby kroków algorytmu).
Niedeterministyczna maszyna Turinga (NDTM) jest zdefiniowana dokładnie w ten sam sposób, co deterministyczna, jednak funkcja przejścia d(q,s) może mieć kilka różnych wartości (efektywnie powodując rozwidlenie działania programu na kilka możliwych ścieżek). Wynik obliczeń jest pozytywny, jeśli choć jedna z możliwych dróg działania maszyny doprowadzi do sukcesu.
Możemy sobie wyobrażać NDTM jako maszynę o nieskończonej możliwości klonowania się i wykonywania wszystkich ścieżek na raz. Możemy też zamiast tego przyjąć, że NDTM podczas wykonywania "programu" potrafi w magiczny sposób przewidzieć, jakiego dokonać wyboru (np. czy zapisać na taśmie 1, czy 0), by doprowadzić do pozytywnego wyniku (o ile jest to w ogóle możliwe). W takim razie jej działanie będzie z zewnątrz przypominało pracę DTM.
O ile DTM może być z dobrym przybliżeniem utożsamiana ze zwykłymi komputerami, to NDTM nie udało się jeszcze nikomu zbudować. Mimo tego pojęcie NDTM ma bardzo pożyteczne własności w teorii złożoności obliczeniowej.
Maszyna Turinga jako ścisły model matematyczny umożliwia precyzyjne definiowanie pojęć związanych ze złożonością obliczeniową. Możemy dzięki temu formalnie zdefiniować następujące pojęcia:
Problem należy do klasy złożoności czasowej P, gdy istnieje DTM rozwiązująca ten problem w czasie wielomianowym względem rozmiaru danych wejściowych.
Problem należy do klasy złożoności czasowej NP, gdy istnieje NDTM rozwiązująca ten problem w czasie wielomianowym względem rozmiaru danych wejściowych.
Problemy z klasy P to m.in. wszystkie te problemy, dla których znamy proste rozwiązania (mnożenie macierzy, sortowanie itp.). Natomiast klasa NP jest mniej intuicyjna. Możemy powiedzieć, że problem ma złożoność NP, jeśli znając rozwiązanie jesteśmy w stanie sprawdzić w czasie wielomianowym, czy jest ono poprawne.
Uwaga (Teza Churcha): Możemy DTM uważać za model dowolnej klasycznej sekwencyjnej maszyny cyfrowej, więc w definicji klasy P możemy napis "DTM" zastąpić słowami "algorytm sekwencyjny".
Uwaga: Analogią NDTM w informatyce mógłby być język programowania ze specjalną funkcją, np. forecast(), zwracającą wartość 0 lub 1 (zawsze w ten sposób, "żeby było dobrze", tzn. żeby na końcu danej ścieżki osiągnąć wynik - jeśli istnieje).
Warto zauważyć, że formalnie klasy NP i P nie muszą być różne. Na pewno wszystkie problemy w klasie P należą też do klasy NP (bo DTM jest szczególnym przypadkiem NDTM). Nie wiemy, czy w klasie NP jest coś więcej, niż w P - por. następny rozdział.
W klasie NP można wyróżnić ciekawą podklasę problemów "uniwersalnych":
Problem P0 jest NP-zupełny, gdy:
Problemy NP-zupełne byłyby więc w pewnym sensie najtrudniejsze w całej klasie NP, gdyż rozwiązując je, rozwiążemy też wszystkie pozostałe problemy. Czyli np. znając rozwiązanie problemu P0 w czasie wielomianowym na DTM, moglibyśmy w czasie wielomianowym rozwiązać każdy problem z klasy NP. Czyli wówczas byłoby P = NP.
Problem NP-trudny to taki problem, który spełnia tylko punkt b) powyższej definicji. Problemy NP-zupełne mają zwykle postać pytania "czy istnieje...", a problemy NP-trudne to zwykle ich optymalizacyjne wersje - "znajdź najmniejszy...".
Okazuje się, że taki uniwersalny (NP-zupełny) problem istnieje i ma dość proste sformułowanie.
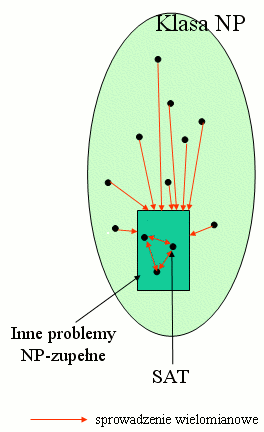Twierdzenie: Sprawdzenie, czy dana formuła logiczna jest spełnialna (problem SAT), jest problemem NP-zupełnym.
Aby się o tym przekonać, musimy sprawdzić oba punkty definicji:
a) Sprawdzenie, czy formuła jest spełnialna (problem SAT), należy do klasy NP.
Zarys dowodu: używamy funkcji forecast(), by znaleźć wartościowanie spełniające formułę. W szybki (wielomianowy) sposób sprawdzamy, że rzeczywiście formuła jest spełniona.
b) Do problemu SAT da się sprowadzić dowolny problem z klasy NP.
Zarys dowodu: każdą maszynę Turinga rozwiązującą konkretny problem z klasy NP (wraz z danymi wejściowymi) można opisać pewną skomplikowaną formułą logiczną, która jest spełnialna wtedy i tylko wtedy, gdy maszyna da wynik pozytywny. Zamiast konstruować maszynę, możemy więc znaleźć odpowiednią formułę i sprawdzić, czy jest spełnialna.
Wniosek: Istnieje problem "uniwersalny" (SAT), tzn. taki, że jego rozwiązanie w czasie wielomianowym pozwalałoby na rozwiązanie wszystkich problemów z klasy NP w czasie wielomianowym.
Okazuje się, że takich problemów NP-zupełnych jest więcej. Niestety, nie znamy algorytmu rozwiązującego SAT o złożoności mniejszej, niż wykładnicza. Nie znamy też takiego algorytmu dla żadnego innego z licznych znanych problemów NP-zupełnych (nie znamy tez dowodu, że takich algorytmów nie ma). Problem, czy klasa P=NP, pozostaje nadal jednym z najważniejszych problemów otwartych informatyki.
Sprawdźmy, że problem istnienia w grafie kliki również jest NP-zupełny.
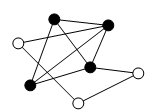Niech G=(V, E) - dany graf. Kliką nazywamy zbiór wierzchołków grafu G połączonych "każdy z każdym".
Problem: Czy w danym grafie istnieje klika rzędu k?
Okazuje się, że problem 3-SAT (czyli problem spełnialności formuł logicznych w postaci koniunkcji klauzul będących najwyżej 3-elementowymi alternatywami literałów) również jest NP-zupełny. Sprowadzimy 3-SAT do problemu kliki.
Niech nasza formuła składa się z k klauzul. Każdy występujący w formule literał ai kodujemy jako jeden wierzchołek w grafie. Wierzchołki łączymy krawędzią, jeśli odpowiednie dwa literały należą do różnych klauzul i nie są wzajemnie sprzeczne (tzn. nie łączymy zmiennej i jej zaprzeczenia).
Wtedy klika rzędu k w tak skonstruowanym grafie odpowiada wartościowaniu spełniającemu formułę.
Stwierdzenie, że pewien problem jest NP-zupełny (lub NP-trudny) oznacza, że bardzo trudne będzie jego rozwiązanie dokładne. Nie znamy algorytmów o złożonosci niższej, niż wykładnicza. W takiej sytuacji uzasadnione jest skupienie sie na rozwiązaniach przybliżonych, oferowanych np. przez heurystyki opisane na poprzednim wykładzie.
Dzięki wprowadzeniu formalnej definicji złożoności obliczeniowej (za pomoca maszyn Turinga), mogliśmy zdefiniowac klasę złożoności P, odpowiadajacą problemom w pewnym sensie prostym, oraz klasę NP, do której należy bardzo dużo problemów praktycznych. Pojęcie problemu NP-zupełnego będzie pomocne do okreslenia, które problemy prawdopodobnie nie mają prostych rozwiązań deterministycznych.
Zalecana literatura:
Szczegółowe definicje znajdują się w treści wykładu (słowa kluczowe zaznaczone są na czerwono).
deterministyczna maszyna Turinga - uproszczony model obliczeń odpowiadający deterministycznemu komputerowi
klasa złożoności NP - problemy, dla których istnieje wielomianowe rozwiązanie przez NDTM
klasa złożoności P - problemy, dla których istnieje wielomianowe rozwiązanie przez DTM
klika - zbiór wierzchołków grafu połączonych "każdy z każdym"
niedeterministyczna maszyna Turinga - uproszczony model obliczeń odpowiadający hipotetycznemu komputerowi dokonujacemu niedeterministycznych (zawsze poprawnych) wyborów
problem NP-trudny - problem równie trudny, jak problemy NP-zupełne, jednak niekoniecznie należący do klasy NP
problem NP-zupełny - problem uniwersalny (najtrudniejszy) w klasie NP
problem SAT - problem istnienia wartościowania spełniającego daną formułę logiczną
złożoność czasowa - liczba kroków algorytmu potrzebna do rozwiązania zadania
złożoność pamięciowa - liczba jednostek pamięci potrzebna do rozwiązania zadania