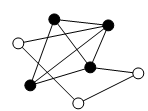
Niech G=(V, E) - dany graf. Kliką nazywamy zbiór wierzchołków grafu G połączonych "każdy z każdym".Klasa problemów NP-zupełnych zdefiniowana na poprzednim wykładzie okazuje się być klasą bardzo szeroką i mającą duże znaczenie praktyczne. Niniejszy wykład stanowi przegląd problemów NP-zupełnych i metod radzenia sobie z nimi.
Przypomnijmy podstawowe pojęcia i fakty poznane na poprzednim wykładzie:
Stwierdzenie, że dany problem jest NP-zupełny oznacza w praktyce, że powinniśmy wykorzystywać przybliżone algorytmy heurystyczne (jak poznany już algorytm zachłanny, wspinaczki czy przeszukiwanie wiązkowe). Udowodnienie, że problem rzeczywiście jest NP-zupełny, bywa dość trudne i wykracza poza ramy tego wykładu - w poniższym zestawieniu problemów ograniczymy się jedynie do zaznaczenia, który z problemów jest NP-zupełny.
Większość popularnych algorytmów heurystycznych (przybliżonych) opiera się na dwóch podstawowych schematach: zachłannym (budowanie rozwiązań po kawałku) i opartym na sąsiedztwie (oceniamy pełne rozwiązania i definiujemy zasady sąsiedztwa). Oznacza to, że aby wskazać sposób rozwiązania problemów za pomocą jednej z poznanych metod (i wielu, które dopiero poznamy), wystarczy omówić te dwa aspekty. W poniższym zestawieniu omówienia te umieszczono w tabelkach.
Problem ten został na poprzednim wykładzie omówiony i przedstawiony jako NP-zupełny. Dla przypomnienia:
Niech G=(V, E) - dany graf. Kliką nazywamy zbiór wierzchołków grafu G połączonych "każdy z każdym".
Problem: Czy w danym grafie istnieje klika rzędu k?
Wersja optymalizacyjna problemu: znaleźć w grafie największą klikę.|
Jeden krok = dodanie do podzbioru kolejnego (wybranego) wierzchołka, łączącego się ze wszystkimi dotychczasowymi. Jakość dodawanego wierzchołka: liczba wychodzących z niego krawędzi. |
Rozwiązania sąsiednie to takie, które różnią się jednym wierzchołkiem (dodanym lub usuniętym z podzbioru). Oceniamy wszystkie podzbiory, również nie będące klikami. Miara jakości: |
Dany jest graf G = (V, E). Znaleźć najmniejszy podzbiór wierzchołków taki, by każda krawędź kończyła się jednym z nich. (Problem NP-trudny)
|
Jeden krok = dodanie do podzbioru wybranego wierzchołka. Jakość dodawanego wierzchołka: liczba nowo pokrytych przez niego krawędzi. |
Rozwiązania sąsiednie to takie, które różnią się jednym wierzchołkiem (dodanym lub usuniętym z podzbioru). Oceniamy wszystkie podzbiory, również nie będące pełnymi pokryciami. Miara jakości: |
Mamy dany zbiór n wartości rzeczywistych {a1, ... , an}. Czy da się podzielić zbiór na dwa rozłączne podzbiory A1 i A2 takie, żeby suma wartości z A1 równała się sumie wartości z A2? (Problem NP-zupełny)
Wersja optymalizacyjna: znaleźć podział dający najmniejszy moduł różnicy sum.
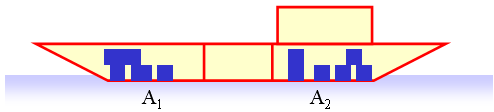
Przykład praktyczny: rozmieścić towar (kontenery o różnej masie) w ładowni dziobowej i rufowej tak, by statek był w równowadze.
|
Jeden krok = dodanie jednego lub dwóch elementów. Jakość jednego kroku: jak najmniejszy moduł różnicy wag po operacji. |
Rozwiązania sąsiednie to takie, które różnią się położeniem jednego lub dwóch elementów. Funkcja celu: moduł różnicy wag. |
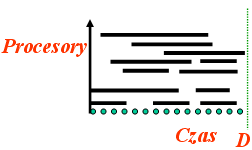
Dany jest zbiór zadań do wykonania (w dowolnej kolejności) o ustalonych długościach, oraz liczba m procesorów. Czy da się rozdzielić i rozplanować zadania tak, żeby się zmieścić w pewnym limicie czasu D? (Problem NP-zupełny)
|
Jeden krok = dodanie jednego zadania. Przydzielamy zadanie pierwszemu procesorowi, który jest wolny (poczynając od najdłuższych zadań). |
Rozwiązania sąsiednie to takie, które różnią się przyporządkowaniem jednego zadania. Funkcja celu: minimalizacja przekroczenia limitu D. |
Znamy problem minimalnego pokrycia macierzy zerojedynkowej. Równoważnym problemem jest problem minimalnego pokrycia zbioru (oba problemy są NP-trudne):
Dany jest zbiór U i rodzina jego podzbiorów {S1, …, Sn}, dająca w sumie U. Znajdź najmniejszą podrodzinę {Sa1, …, Sak} taką, że suma tej podrodziny również wynosi U.
|
Jeden krok = dodanie jednego podzbioru. Wybieramy ten podzbiór, który pokrywa jak największą niepokrytą część U. |
Rozwiązania sąsiednie to takie, które różnią się jednym elementem. Oceniamy wszystkie rozwiązania, również nie będące pełnymi pokryciami. Miara jakości: |
Metody typu przeszukiwanie tabu czy algorytm wspinaczki bazują na pojęciu sąsiedztwa rozwiązań (punktów przestrzeni stanów). Może być ono zdefiniowane przez nas w zasadzie dowolnie, jednak należy trzymać się kilku zasad ogólnych:
Przykład: problem podziału zbioru.
Mamy dany zbiór n wartości rzeczywistych {a1, ... , an}. Znaleźć podział zbioru na dwa rozłączne podzbiory A1 i A2 taki, żeby moduł różnicy sum wartości z A1 i A2 był minimalny.
Funkcja celu: moduł różnicy sum zbiorów (minimalizujemy).
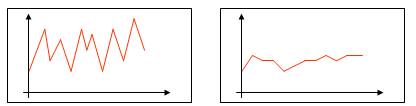
Jeżeli sąsiednie rozwiązanie polega na tym, że przekładamy jeden pakunek z jednej ładowni do drugiej, to taka funkcja jest trudna do optymalizacji (lewy wykres), gdyż ma wiele maksimów lokalnych.
Jeżeli sąsiednie rozwiązanie polega na tym, że wybieramy parę pakunków z różnych ładowni i zamieniamy je miejscami, wówczas zmiany funkcji celu są łagodniejsze (prawy wykres), ale relacja jest niespójna (nie zmieniamy liczby pakunków w żadnej z ładowni). Dodatkowo zamiast n sąsiadów mamy ich rzędu n2.
Najlepiej połączyć te dwie definicje sąsiedztwa w jednym algorytmie.
Zaprezentowano przegląd problemów optymalizacyjnych wraz z uniwersalnymi schematami ich rozwiązania. Problemy te odpowiadają bardzo wielu praktycznym zadaniom optymalizacyjnym. Pominięto (omówione na jednym z poprzednich wykładów) problem komiwojażera i problem pokrycia macierzy.
Zalecana literatura:
7.1. Sprawdzić, że miary jakości rozwiązań dla problemów opisanych na tym wykładzie osiągają wartość maksymalną dla rozwiązania optymalnego.