Wstęp
Niezależnie od tego czy warstwa sieci świadczy usługę opartą na datagramach czy wirtualnych obwodach aby zrealizować ją poprawnie musi być w stanie określić ścieżkę z której mają korzystać pakiety w drodze od nadawcy do odbiorcy. Oczywiście samo znalezienie ścieżki nie gwarantuje efektywnej komunikacji, ważne jest aby była to dobra ścieżka. Zupełnie inną sprawą jest wyjaśnienia pojęcia dobra. Czasami chodzi nam o ścieżki o najniższym koszcie, innym razem istotne jest opóźnienie a jeszcze innym niezawodność łącza. Czasami trzeba uwzględnić także pewne ograniczenia takie jak to, że router należący do organizacji Z nie powinien przesyłać żadnych pakietów należących do organizacji Y. Jednym ze sposobów klasyfikowania algorytmów routingu jest podzielenie ich ze względu na poziom wiedzy (globalny lub lokalny):
- globalny algorytm routingu algorytm taki określa ścieżkę o najmniejszym koszcie między węzłem źródłowym i docelowym za pomocą globalnej wiedzy na temat sieci; głównym problemem jest to, że algorytm musi w jakiś sposób uzyskać wiarygodne informacje o całej sieci; obliczenia mogą być już później przeprowadzone lokalnie,
- zdecentralizowany algorytm routingu w takich algorytmach wyznaczanie ścieżki o najmniejszym koszcie przebiega iteracyjnie; każdy z węzłów dokonuje części obliczeń i ma tylko wycinek informacji (przetwarzanie rozproszone),
Innym sposobem klasyfikacji algorytmów routingu jest podział na statyczne, w których trasy bardzo wolno ulegają zmianom (najczęściej są one powodowane interwencjami użytkownika; ręczną edycją tabel routingu) i dynamiczne, w których tablice routingu zmieniane są automatycznie i na bieżąco wraz ze zmianami topologii sieci. Algorytmy dynamiczne choć charakteryzują się większą szybkością dostosowywania się do zmian są jednocześnie bardziej podatne na pętle routingu i wahania związane z trasami.
Algorytm Dijkstra
Algorytm Dijkstra został opracowany przez holenderskiego matematyka Edsgera Dijkstrę (ur. 1930, zm. 2002). Służy on do znajdowania najtańszych ścieżek w grafie łączących jeden, wybrany węzeł ze wszystkimi pozostałymi węzłami. Nie można go stosować do grafów, których krawędzie mają ujemne wagi. W takim wypadku należy użyć bardziej ogólnego algorytmu Bellmana-Forda. Jeśli wszystkie krawędzie w grafie mają wartość 1 to istnieje prostszy algorytm znajdowania najkrótszej ścieżki algorytm przeszukiwania grafu wstecz. Jako efekt działania algorytmu otrzymujemy najkrótsze ścieżki tylko i wyłącznie z węzła, który wybraliśmy jako startowy, a nie wszystkie najkrótsze ścieżki pomiędzy dowolnymi dwoma węzłami w grafie.
Sposób działania algorytmu
Rysunek 1 przedstawia przykładowy graf. Załóżmy, że szukamy najkrótszych ścieżek z węzła A (nie jest to wcale regułą i zamiast A moglibyśmy wybrać dowolny inny węzeł, z którego chcielibyśmy znaleźć najkrótsze ścieżki). Rozwiązania zadania zostało przedstawione w tabelce 1. W pierwszym kroku obliczamy odległość do węzłów, do których możemy dotrzeć bezpośrednio z A. Wyniki wpisujemy w tabelkę.
Dla pierwszego wiersza mamy w kolejnych kolumnach:
- odległość do węzła B wynosi D(B)=2, a poprzedni węzeł z którego dotarliśmy do tego węzła to P(B)=A,
- nie możemy dojść bezpośrednio z węzła A do węzła C w związku z tym odległość oznaczamy jako nieskończoność,
- nie możemy dojść bezpośrednio z węzła A do węzła D w związku z tym odległość oznaczamy jako nieskończoność,
- odległość do węzła E wynosi D(E)=10, a poprzedni węzeł z którego dotarliśmy do tego węzła to P(E)=A,
- nie możemy dojść bezpośrednio z węzła A do węzła F w związku z tym odległość oznaczamy jako nieskończoność,
W ten sposób udało się nam wypełnić pierwszy wiersz tabelki. W kolejnym kroku wybieramy węzeł, do którego mamy najbliżej (jeśli do dwóch węzłów odległość jest taka sama możemy wybrać dowolny z nich). W naszym zadaniu jest to węzeł B, bo 2 jest mniejsze od 10. Po wybraniu kolejnego węzła dodajemy go do ścieżki, która jest wpisana w kolumnę węzły. Ponownie obliczamy odległość do pozostałych węzłów, tym razem jednak nasz zasięg rozszerzył się o możliwość przejścia przez węzeł, który właśnie dodaliśmy do ścieżki (w tym przypadku B). W związku z tym dla drugiego wiersza kolejno od lewej mamy:
- ponieważ węzeł B jest częścią ścieżki to nie musimy mierzyć odległości do niego; stawiamy po prostu kreskę,
- do węzła C możemy dojść z węzła A przechodząc przez węzeł B, koszt takiego przejścia to P(C)=4 (bo A->B=2 i z B->C=2 więc w sumie 4); węzłem z którego bezpośrednio doszliśmy do C jest P(C)=B,
- nie możemy dojść bezpośrednio z węzła A do węzła D w związku z tym odległość oznaczamy jako nieskończoność,
- odległość do węzła E pozostaje bez zmian i wynosi D(E)=10, a poprzedni węzeł z którego dotarliśmy do tego węzła to P(E)=A,
- do węzła F możemy dojść z węzła A przechodząc przez węzeł B, koszt takiego przejścia to P(F)=5 (bo A->B=2 i z B->=3 więc w sumie otrzymujemy 5), węzłem z którego bezpośrednio doszliśmy do F jest P(F)=B,
W kolejnym kroku wybieramy węzeł C ponieważ odległość do niego (4) jest najmniejsza. W związku z tym mamy w kolumnie węzły wpis ABC. Obliczamy dystans do poszczególnych węzłów. Warto zauważyć, że po raz pierwszy możemy dojść do węzła D poprzez węzły B i C. W czwartym wierszu wybieramy węzeł F, bo 5 jest mniejsze od 10 i 12. W związku z tym dla czwartego węzła mamy odpowiednio:
- ponieważ węzeł B jest częścią ścieżki to nie musimy mierzyć odległości do niego; stawiamy po prostu kreskę,
- ponieważ węzeł C jest częścią ścieżki to nie musimy mierzyć odległości do niego; stawiamy po prostu kreskę,
- dzięki temu, że dołączyliśmy węzeł F pojawiła się nowa, krótsza od poprzedniej ścieżka do węzła D (od węzła A); przechodzi ona przez węzły B i F, a jej długość wynosi P(D)=8; poprzednim węzłem jest natomiast D(D)=F,
- podobnie jak w poprzedniej kolumnie, także w tej dołączenie węzła F spowodowało, że powstała krótsza droga do węzła E; przechodzi ona przez węzły B i F i ma długość P(E)=6; poprzednim węzłem jest natomiast D(E)=E,
- węzeł F jest już częścią ścieżki więc nie musimy mierzyć odległości do niego; stawiamy tam kreskę,
W kolejnym kroku wybieramy węzeł E, a jeszcze następnym F. Procedurę powtarzamy, aż dołączymy wszystkie węzły do ścieżki. Wtedy w ostatnim wierszu muszą pojawić się same kreski. Otrzymaliśmy tablicę, która umożliwi wyznaczenie nam najkrótszej ścieżki (zarówno jeśli chodzi o jej długość jak i węzły przez które przechodzi) pomiędzy węzłem A i dowolnym innym węzłem w grafie.
Znajdowanie najkrótszej drogi pomiędzy węzłem A a węzłem D odbywa się w sposób następujący:
- odnajdujemy kolumnę, która dotyczy węzła D (w naszej tabeli jest to 4 kolumna) i odczytujemy ostatni wpis w tej kolumnie (taki, który nie jest kreską); w tym przypadku mamy 8,F,
- z odczytanej w poprzednim punkcie wartości bierzemy poprzednik (F) i odnajdujemy kolumnę, którą on identyfikuje (w tym przypadku jest to ostatnia kolumna), znów odczytujemy ostatni wpis w tej kolumnie 5,B,
- z poprzedniego kroku znów bierzemy identyfikator poprzednika (B) i odnajdujemy odpowiednią kolumnę (druga kolumna); odczytujemy ostatnią wartość (2,A);
- identyfikator poprzednika w punkcie powyżej jest A; jest to jeden z końców naszej poszukiwanej drogi w związku z tym kończymy algorytm i możemy wypisać najkrótszą ścieżkę od A do D; najkrótsza ścieżka składa się z czterech węzłów: A->B->F->D, są to kolejne znalezione przez nas poprzedniki podczas realizacji tego algorytmu,
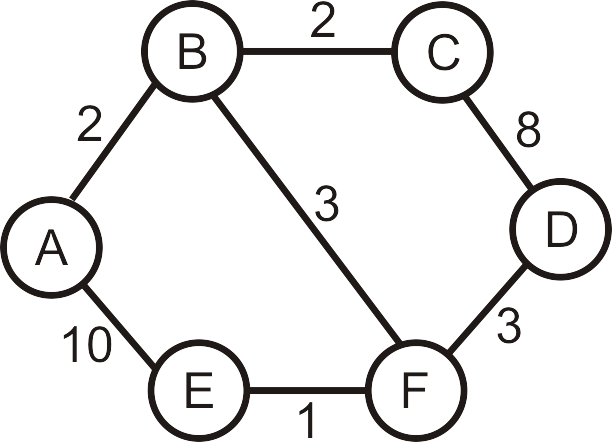
Rys.1. Przykładowa sieć
| Węzły | D(B), P(B) | D(C), P(C) | D(D), P(D) | D(E), P(E) | D(F), P(F) |
| A | 2,A | niesk. | niesk. | 10,A | niesk. |
| AB | ------ | 4,B | niesk. | 10,A | 5,B |
| ABC | ------ | ------ | 12,C | 10,A | 5,B |
| ABCF | ------ | ------ | 8,F | 6,E | ------ |
| ABCFE | ------ | ------ | 8,F | ------ | ------ |
| ABCFED | ------ | ------ | ------ | ------ | ------ |